实验3

实验3.1 （主元的选取与算法的稳定性）

问题提出：Gauss消去法是我们在线性代数中已经熟悉的。但由于计算机的数值运算是在一个有限的浮点数集合上进行的，如何才能确保Gauss消去法作为数值算法的稳定性呢？Gauss消去法从理论算法到数值算法，其关键是主元的选择。主元的选择从数学理论上看起来平凡，它却是数值分析中十分典型的问题。

实验内容：考虑线性方程组

编制一个能自动选取主元，又能手动选取主元的求解线性方程组的Gauss消去过程。

实验要求：

（1）取矩阵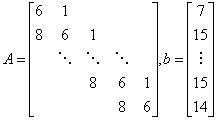，则方程有解。取n=10计算矩阵的条件数。让程序自动选取主元，结果如何？

（2）现选择程序中手动选取主元的功能。每步消去过程总选取按模最小或按模尽可能小的元素作为主元，观察并记录计算结果。若每步消去过程总选取按模最大的元素作为主元，结果又如何？分析实验的结果。

（3）取矩阵阶数n=20或者更大，重复上述实验过程，观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异，说明主元素的选取在消去过程中的作用。

（4）将上述矩阵A中的主元改为0.00006再重新作一次数值实验看看。

（5）选取其他你感兴趣的问题或者随机生成矩阵，计算其条件数。重复上述实验，观察记录并分析实验结果。

实验3.2（线性代数方程组的性态与条件数的估计）

问题提出：理论上，线性代数方程组的摄动满足

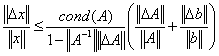
矩阵的条件数确实是对矩阵病态性的刻画，但在实际应用中直接计算它显然不现实，因为计算通常要比求解方程还困难。

实验内容：MATLAB中提供有函数“condest”可以用来估计矩阵的条件数，它给出的是按1-范数的条件数。首先构造非奇异矩阵A和右端，使得方程是可以精确求解的。再人为地引进系数矩阵和右端的摄动，使得充分小。

实验要求：

（1）假设方程Ax=b的解为x，求解方程，以1-范数，给出的计算结果。

（2）选择一系列维数递增的矩阵（可以是随机生成的），比较函数“condest”所需机器时间的差别.考虑若干逆是已知的矩阵，借助函数“eig”很容易给出cond₂(A)的数值。将它与函数“cond(A,2)”所得到的结果进行比较。

（3）利用“condest”给出矩阵A条件数的估计，针对（1）中的结果给出的理论估计，并将它与（1）给出的计算结果进行比较，分析所得结果。注意，如果给出了cond(A)和的估计，马上就可以给出的估计。

（4）估计著名的Hilbert矩阵的条件数。

思考题一：（Vadermonde矩阵）设

，

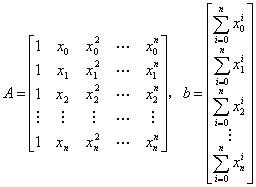其中，，

（1）对n=2,5,8，计算A的条件数；随n增大，矩阵性态如何变化？

（2）对n=5，解方程组Ax=b；设A的最后一个元素有扰动10^-4，再求解Ax=b

（3）计算（2）扰动相对误差与解的相对偏差，分析它们与条件数的关系。

（4）你能由此解释为什么不用插值函数存在定理直接求插值函数而要用拉格朗日或牛顿插值法的原因吗？