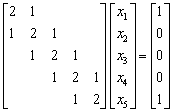1．填空题
(1) 设x = (1, -1, 2)T，那么
，
，
(2) 设矩阵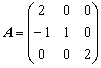
，那么
，
(3) 矩阵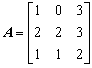
，则A的条件数
(4) 已知A为n阶对称矩阵，且ρ(A) = 3，那么
(5) 线性方程组的性态是衡量方程组的解对扰动（误差）的敏感程度的，若较小的扰动带来解的较大变化，那么称方程组是病态的，否则称为良态的．一般如果系数矩阵A的条件数cond(A) 
时，方程组是病态的.
(6) 对任一n维向量x =(x1, x2,…,xn)T，不同的范数，其值不同，但总满足下面关系式
2．判断题
(1) 对任何非奇异矩方阵A，都有cond (A) ≥ 1. ( )
(2) 对任何非奇异矩方阵A的任一范数，都有ρ(A) ≥ ||A||. ( )
(3) 若线性方程组的系数矩阵A的各元素间量级差异很大且无一定规律，或者某些行（列）近似线性相关，则方程组可能为病态的． ( )
(4) 方程组的性态是其固有性质，任何方法都不可能改变其病态程度．
( )
3．设矩阵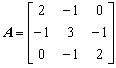
，求||A||p ( p = 1, 2, ∞)和ρ(A)．
4．证明：对于矩阵A范数，如果
，则：
5．填空题
(1) 已知线性方程组Ax = b为：
① 给右端项b一扰动
，取无穷大范数，利用公式
估计解x的相对误差，求得
，
， 
从而
② 给系数矩阵A一扰动
，取无穷大范数，利用公式
估计解x的相对误差，求得
从而
(2) 希尔伯特（Hilbert）矩阵（又称坡度阵）
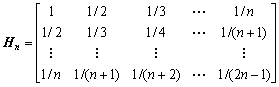是有名的病态阵，当n = 3时，
，且随着阶数的增大，条件数迅速增大．
6．给定线性方程组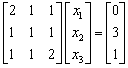
(1) 分别写出雅可比和高斯-塞德尔迭代格式，并判断它们的收敛性.
(2) 取初值x (0) = (0, 0, 0)T，用(2)中收敛的迭代格式求解（保留到小数点后4位）．
7．填空题
(1) 将方程组
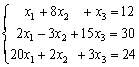
中方程的顺序由“①-②-③”调整为
能使雅可比和高斯-塞德尔迭代收敛．
(2) 用高斯-塞德尔迭代法求解线性方程组
那么迭代格式
．（填“收敛”或“不收敛”）
(3) 解线性方程组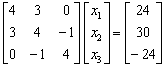
的高斯-赛德尔迭代格式为
8．判断题
(1) 对线性方程组Ax = b构造的雅可比、高斯-塞德尔和超松弛迭代格式的收敛性仅与方程组的系数矩阵A有关，而与迭代初值x (0)无关． ( )
(2) 高斯-塞德尔迭代格式一定比雅可比迭代格式收敛速度快． ( )
(3) 若方阵A严格对角占优，则A非奇异．
( )
(4) 对收敛的迭代格式，在迭代计算的过程中，不怕中途出错．
( )
9．对方程组
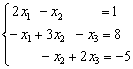
用超松弛迭代（取ω = 1.1）求解，取初值x(0) = (0, 0, 0)T，并精确到小数点后3位.
9．分别用高斯消去法，列主元消去法解下列方程组（（1），（2）用具有舍入的位浮点数进行计算，（3）用于浮点数计算），并比较计算结果。
（1）
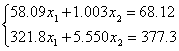
（2）
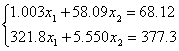
（3）
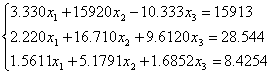
10.
设有线性方程组
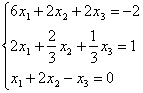
试用高斯消去法，列主元消去法，完全选主元消去法解此方程组（且具有舍入的位浮点数进行计算），比较计算结果。
11．设
为对称矩阵，且
，经高斯消去法一步后，A约化为
试证明
亦是对称矩阵。
12．设
，其中U为上三角阵（或下三角阵。）
（1）计算解所需要的乘除法次数。
（2）设
为非奇异的上三角阵，试推导求
的递推公式。
13．设
是指标为
的初等下三角阵，求证：当
时，则
也是一个指标为的初等下三角阵。
14.试推导矩阵
的Crout分解
的计算公式，其中
为下三角阵，
为单位上三角阵。
15．设为对称正定，试证明
（1）的对角元素，
（2）经过高斯消去法一步，约化为
则亦是对称正定阵。
16．用高斯-约当方法求A的逆：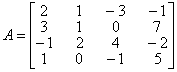
17．用改进的平方根法解方程组：
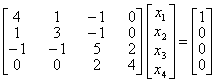
18．用追赶法解方程组：
19．试用部分选主元三角分解法解方程组：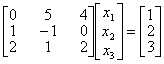
20．设：
，(1)计算
。
（2）计算
，及
21．设
，其中为非奇异矩阵，则
（1）
为对称正定矩阵。
（2）
。
22．设
，求证：（1）
(2)
23.如果P为正交矩阵，求证
。
24．选择题
当n阶方阵A满足条件（ ）时，线性方程组Ax = b有唯一解.
(A) A非奇异 (B)
R(A) ≠ 0
(C) R(A)
< n (D)
以上都不对
25．填空题
(1) 如果一种算法在计算中舍入误差积累迅速增长，无法控制，造成结果失真，则称这一算法是数值不稳定的，反之是数值稳定的.高斯消去法是
的算法.
(2) 解线性方程组的直接法有消去法与列主元消去法，其中
有利于控制误差的增长，这是因为它能有效克服“小”主元带来的
现象，从而有效控制误差的增长.
(3) 过三点(1, 1)、(2, -1)和(3, 1)的抛物线为
(4) 用列主元高斯消去法，对方程组的增广矩阵作初等变换，当进行至
时，下一步所选主元为
26．用高斯消去法求解方程组：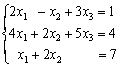
27．用列主元消去法求解方程组（计算结果保留到小数点后3位）
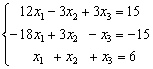
28．判断题
(1) 当矩阵A的各阶前主子式都不等于零时，可唯一地分解为一个单位下三角阵L和一个上三角阵U的乘积． ( )
(2) 若不计舍入误差，LU分解法是求解线性方程组的精确方法． ( )
(3) LU分解法中的U就是高斯消去法得到的上三角方程组的系数矩阵． ( )
29．用矩阵的LU分解法求解线性方程组Ax = b，其中
， 
30．用LU紧凑格式分解法求解线性方程组Ax = b，其中
， 
31．选择题
(1) 当矩阵A满足条件（ ）时，解方程组Ax = b的LU分解法就可用改进的平方根法（或称改进的乔累斯基分解法）来求解，从而减少计算量.
(A) A对称正定 (B)
A的所有顺序主子式都大于零
(C) 选项(A)、(B)结合 (D)
A非奇异
(2) 当方程组Ax = b的系数矩阵为三对角矩阵时，由对A的LU分解公式，可得到求解三对角方程组的（ ）
(A) 乔累斯基分解法 (B)
追赶法
(C) LDLT分解法 (D)
以上选项都不对
32．填空题：用改进的平方根法（或改进的乔累斯基分解法）求解线性方程组：
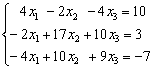
对其增广矩阵进行如下的紧凑格式分解：
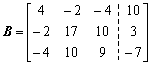
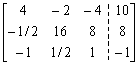
得到等价的三角形方程组为
， 回代解得
33．用追赶法求解方程组：