1．填空题
(1) 过点(0, 2)、(1, 1)、(2, 2)的不超过2次的多项式为
(2) 设xi (i = 0, 1, 2, …, n)为n+1个互异的插值节点，li(x)为相应的Lagrange插值基函数，则
(3) 设xi = i (i = 0, 1, 2, …, n)为n+1个互异的插值节点，li(x)是相应的n次Lagrange插值基函数，则
(4) 设li(x)是对n+1个点xi (i = 0, 1, 2, …, n)进行Lagrange插值的基函数，则
(5) 如果记R(x)为过两点(x0, y0)、(x1, y1)的插值多项式P1(x)的余项，则R(x)的误差限为
(6) 多项式
和 
都能插值下表
|
xi |
1 |
2 |
3 |
4 |
|
yi |
2 |
1 |
6 |
47 |
这是否违背插值多项式的唯一性？
（填“是”或“否”）
2．给定数据表
|
x |
0 |
2 |
3 |
5 |
|
f (x) |
1 |
-3 |
-4 |
2 |
用拉格朗日插值方法求出f (x)的不超过3次的插值多项式L3(x)．
3．将下面计算过程补充完整。给定函数sinx的数值表如下
|
x |
0.32 |
0.34 |
0.36 |
|
sinx |
0.314567 |
0.333487 |
0.352274 |
用线性插值和抛物线插值计算sin0.3367的值，并利用插值余项给出计算结果的误差限．取
x0 =
0.32，y0 = 0.314567； x1 = 0.34，y1 = 0.333487； x2 =
0.36，y2 = 0.352274
(1) 线性插值：由于0.32<0.3367<0.34，在区间[x0, x1]上进行插值，求得
， 
从而
由于
，因而
(ξ∈[0.32, 0.34]
)
(2) 抛物线插值：求得 
，
从而
由于
，因而
(ξ∈[0.32, 0.36]
)
4．已知多项式
通过下列点：
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
p(x) |
31 |
5 |
1 |
1 |
11 |
61 |
试构造一多项式q(x)且通过下列各点：
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
q(x) |
31 |
5 |
1 |
1 |
11 |
1 |
5．填空题
(1) 设f (x)
= an x n +1(an ≠ 0)，则
(2) 设f (x)
= x2+2x，则
，
(3)
对函数表
|
x |
-1 |
0 |
1 |
2 |
|
f (x) |
1 |
-2 |
5 |
10 |
求得其各阶差商如下表
|
x |
f (x) |
一阶差商 |
二阶差商 |
三阶差商 |
|
|
-1 0 1 2 ( ) |
1 -2 5 10 (
) |
-3 7 5 ( ) |
5 -1 (
) |
-2 (
) |
( ) |
那么过这四个点的牛顿插值多项式为
对新增节点x = 3，f (x) = 25，请完成上面的差商计算表；并写出过这五个节点的牛顿插值
多项式
6．判断题
(1)
交换差商f [x0, x1,…,
xk]中的任意两个节点，差商的值改变符号． (
)
(2) 若在原有数据上增加一组数据，则使用牛顿插值的插值多项式只增加一项，不必重复计算所有系数． (
)
(3) 对同一个插值问题，其牛顿插值多项式与拉格朗日多项式相同，且两种余项也相同. (
)
7．给定数据表
|
x |
0 |
2 |
3 |
5 |
|
f (x) |
1 |
-3 |
-4 |
2 |
(1) 求出f (x)的不超过3次的插值多项式.
(2) 若增加一组数据 (4, -1)，求f (x)的不超过4次的插值多项式，并求f (1.5)的近似值．
8．完成下面计算过程
已知单调连续函数y = f (x)的如下数值表
|
x |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
|
f (x) |
0.1995 |
0.3965 |
0.5881 |
0.7721 |
0.9461 |
用反插值插值方法求方程f (x) = 0.4500在(0.00, 1.80)内的根的近似值．
将y作为自变量，采用牛顿插值，完成下面均差表
|
f(xi) |
xi |
一阶均差 |
二阶均差 |
三阶均差 |
四阶均差 |
|
0.1995 0.3965 0.5881 0.7721 0.946 1 |
0 0.2 0.4 0.6 0.8 |
(
) (
) (
) (
) |
(
) (
) (
) |
(
) (
) |
(
) |
从而得到4次插值多项式为
×(y - 0.1995)+×(y - 0.1995)(y - 0.3965)
+×(y - 0.1995)(y - 0.3965)(y - 0.5881)
+×(y - 0.1995)(y - 0.3965)(y -
)(y - 0.7721)
于是方程f (x)
= 0.4500的根为
9．对函数
在区间[1, 2]上作等距分段线性插值，怎样选择步长h，才能使插值误差小于
？
10已知y=f(x)函数表
试用1次，2次，3次Lagrange插值多项式计算f(2.5)近似值。
11 已知f(x)=ex
且函数表为
试用1次，2次，3次Lagrange插值多项式计算f(2.5)近似值。
12．设
为
上具有权函数
的正交多项式组且
为首项系数为1的
次的多项式，则于线性无关。
13．选择
，使下述积分取得最小值
14．设
试用
求
一次最佳平方逼近多项式。
15．设试用Chebyshev多项式
求一次最佳平方逼近多项式。
16．设
，且周期为
，取三角函数正交基
，试求于
在S中最佳平方逼近函数。
17．设已知
函数表
（
）取
,求在
中最小二乘逼近多项式（取权系数
）。
（
）用数学模型 
，求
使：
且比较
两种模型，哪一种更符合数据表的趋势。
18．已知函数表：
试用最小二乘法确定经验公式
中参数
。
19．什么常数C能使得以下表达式最小？
20．如何选取
上与零偏差最小？
21．设
上求3次最佳一致逼近多项式。
22．在
上利用幂数项数缩减求
的3次逼近多项式。使误差不超过0.005。
23．将下函数在展开为切比雪夫级数
24．设
其中
当已计算出系数
及已知
时可由下述递推公式计算数列
即
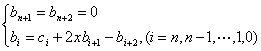
则
。
25．用最小二乘法求解矛盾方程组：