1

1．填空题

(1) 对初值问题

若函数f ( x, y )满足条件，则解y = y ( x )存在且唯一．

(2) 在区间[0, 1]上用欧拉方法求解初值问题

取步长h = 0.1，其差分格式为

(3) 初值问题的梯形公式

是阶方法，是式的方法．（填“显式”或“隐式”）

(4) 对于微分方程初值问题

的差分方法，如果当h→0时，其整体阶段误差e_i→0时，则该方法是的，欧拉方法是的方法．（填“收敛”或“不收敛”）

(5) 改进的欧拉方法的整体截断误差为O(h²)，局部截断误差为

2．用欧拉公式计算初值问题

的解函数y = y (x)在x = 0.1，0.2，0.3处的近似值（保留4位小数）．

3．完成下面计算过程：用改进的欧拉公式求初值问题

的数值解（保留6位小数）．取h = 0.1，由于改进的欧拉公式为

因此该问题的计算格式为

计算结果填入下表

n	x_n	y_n	y_p	y_c
0	0
1	0.1
2	0.2
3	0.3
4	0.4
5	0.5

4．试导出求解初值问题：

的隐式欧拉格式：，并估计其局部截断误差．

5．选择题

(1) 求解常微分初值问题的中点格式

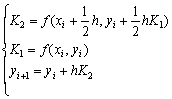
的局部截断误差为（）

(A) O(h) (B) O(h²)

(2) 求解常微分方程初值问题的数值公式

是（）

(A) 单步二阶法 (B) 多步二阶法

(3) 经典的四阶龙格-库塔（Runge-Kutta）方法的局部截断误差为（）

(A) O(h²) (B) O(h³)

6．填空题

(1) 龙格-库塔方法的基本思想是：通过对不同点上f (x, y)的函数值的来构造近似公式的，若有m个点，则其局部截断误差为

(2) 用四阶经典龙格-库塔方法求解初值问题

时，取h = 0.1，得y(1)的近似值为0.42671，而取h = 0.05，得y(1)的近似值为0.43382，若不考虑舍入误差，则y(1)的更好的近似值是

7．取步长h = 0.4，写出用经典四阶龙格-库塔方法求解初值问题

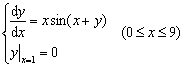
的计算公式．

8．填空题

(1) 用经典的3阶龙格-库塔方法解初值问题

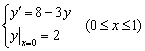
取步长h = 0.2，则，

(2) 用3阶库塔格式

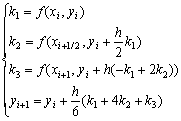
求解初值问题

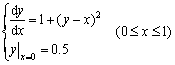
取步长h = 0.1，该方程的库塔计算格式为

取5位小数，计算y (0.1)的近似值，将初值代入得

，，

因此。

9．取h = 0.4，用经典四阶龙格-库塔方法求初值问题

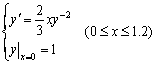
的数值解，并与准确解进行比较．

10 分别是初值问题

及摄动问题

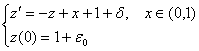
试证明。

11 用均匀步长梯形方法求解：

证明其数值解为且当时（精确解）。

12 证明Heun方法：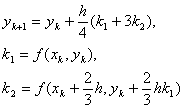

是二阶精度方法，并求出其主局部截断误差项。

13 试证明计算方法

不论如何取，不可能成为三阶方法。

14 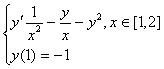试用显示Euler方法，二阶显式Runge－Kutta方法及经典Runge－Kutta方法计算初值问题：

并在处与精确解进行比较。

15.试用经典Runge－Kutta方法计算初始点，再用四阶Adams预估－校正方法计算常微分方程组初值问题（取）

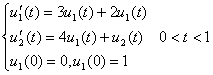
并与精确解比较。

16 确定二步法：

的（1）主局部截断误差；（2）方法的阶；（3）特征多项式；（4）绝对稳定区间。

17 试求系数使用三步法：

的阶尽量高，并写出其主局部截断误差。