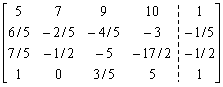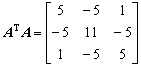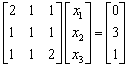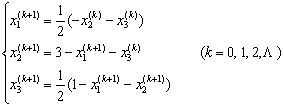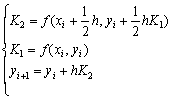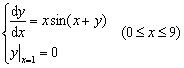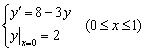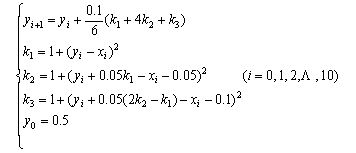第一章 绪论
1.填空题
(1) 如下各数分别作为π的近似值,各有几位有效数字?
3.14 的有效位数是 
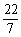 的有效位数是
的有效位数是
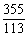 的有效位数是
的有效位数是
(2) 设近似数x*有2位有效数字,则其相对误差限等于 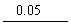
(3) 已知近似数x*的相对误差限为 ,则x*的有效位数至少是
,则x*的有效位数至少是 
(4) 在浮点数系F(2, 8, -7, 8)中共有 个数.
个数.
(5) 现代科学的三大组成部分有:科学实验、理论研究和 科学计算
(6) 误差的四种主要来源有:模型误差、观测误差、 截断 误差 和 舍入 误差,而数值计算仅讨论 截断 误差 和 舍入 误差.
(7) 构造数值稳定的算法,应坚持以下几个原则:
① 要 防止大数“吃掉”小数
② 要 控制舍入误差的传播和积累
③ 要 避免两个相近的数相减
④ 要 避免绝对值很小的数做分母
⑤ 要 减少运算次数,避免误差积累
2.利用等价变换或舍弃高阶无穷小改变下列表达式,使其计算结果比较精确(其中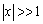 表示
表示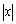 充分大,
充分大, 表示x充分接近0).
表示x充分接近0).
(1)  ,
,
解 原式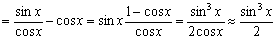
(2)  ,
, 
解 原式
3.设3个近似数a = 3.65,b = 9.81,c = 1.21均有3位有效数字,试计算ac + b,并估计它的绝对误差限、相对误差限和有效数字的位数.
解 ac + b
= 14.2265
由a,b,c有3位有效数字,知其绝对误差da,db,dc均不超过 ,所以
,所以
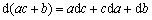


即绝对误差限为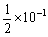 ,说明ac + b
= 14.2265有3位有效数字,ac + b ≈ 14.2
,说明ac + b
= 14.2265有3位有效数字,ac + b ≈ 14.2

所以相对误差限约等于0.21%.
4.填空题
(1) 在浮点数系F(10, 5, -10, 10)中计算 ,可按以下两种顺序进行:
,可按以下两种顺序进行:
① 依k递增的顺序计算
② 依k递减的顺序计算
其中能获得较准确结果的方法编号为 ②
(2) 用四舍五入原则写出下列各数的具有五位有效数字的近似数:
0.7000400 ≈ 0.70004
0.00063217500 ≈ 0.00063218
3.0000098 ≈ 3.0000
314.3569 ≈ 314.36
(3) 用计算机计算n次多项式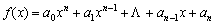 的值,采用秦九韶算法要做 n 次乘法运算,而直接计算需要作
的值,采用秦九韶算法要做 n 次乘法运算,而直接计算需要作 次乘法运算.
次乘法运算.
5.下表中左边第一列各数都是由准确值经四舍五入所得的近似数,试分别将它们的绝对误差限、相对误差限和有效数字的位数写入相应的位置:
|
近似数
|
绝对误差限
|
相对误差限
|
有效数字的位数
|
|
31000
|
0.5
|
0.000016
|
5
|
|
2.3316
|
0.00005
|
0.000021
|
5
|
|
0.5504
|
0.00005
|
0.000091
|
4
|
|
0.001230
|
0.0000005
|
0.00041
|
4
|
6.用秦九韶算法计算当 x = -3时多项式 的值.
的值.
解  ,
, ,
,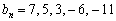 ,
,
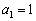 ,
, ,
, ,
, ,
,
即要求的多项式的值为-20.
7.在浮点数系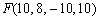 中,已知
中,已知 ,
,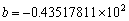 ,
,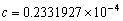 ,分别计算
,分别计算 和
和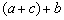 ,并求各结果与精确结果的绝对误差.
,并求各结果与精确结果的绝对误差.
解 


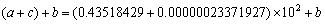

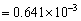
与精确值 比较,二者的绝对误差分别为
比较,二者的绝对误差分别为


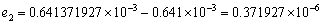
8.设 ,试求函数
,试求函数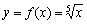 的相对误差限.
的相对误差限.
解 因为 ,
,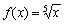 ,
, ,
,
所以 的相对误差限为
的相对误差限为

第二章 非线性方程组的数值解法
9.填空题
(1) 用二分法求方程f(x) = 0的近似根,若f(x)在[a, b]上满足 连续、单调 且 ,则方程在[a, b]上有且仅有一个实根x*
,则方程在[a, b]上有且仅有一个实根x*
(2) 在二分法的误差分析中,因为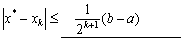 ,所以要使
,所以要使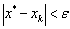 成立,只需
成立,只需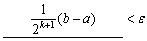 即可
即可
(3) 使用二分法求非线性方程f (x) =
0在[0,
1]内的根,要使误差小于 ,至少要二分区间
,至少要二分区间 次
次
10.用二分法解方程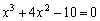 在[1, 2]内的根,要求精确到小数点后第二位,即误差不超过
在[1, 2]内的根,要求精确到小数点后第二位,即误差不超过 .
.
解  ,由
,由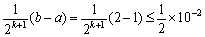 ,得k+1≥7,所以迭代7次即可.计算结果如下表:
,得k+1≥7,所以迭代7次即可.计算结果如下表:
|
k
|
ak
|
bk
|
xk
|
f(xk)的符号
|
|
0
|
1
|
2
|
1.5
|
+
|
|
1
|
1
|
1.5
|
1.25
|
-
|
|
2
|
1.25
|
1.5
|
1.375
|
+
|
|
3
|
1.25
|
1.375
|
1.3125
|
-
|
|
4
|
1.315
|
1.375
|
1.34375
|
-
|
|
5
|
1.34375
|
1.375
|
1.359375
|
-
|
|
6
|
1.359375
|
1.375
|
1.367188
|
|
所以取方程的近似根为 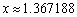 .
.
2.3 简单迭代法
11.为用简单迭代法解方程 在区间[1, 2]上的根,构造了如下3个迭代函数:
在区间[1, 2]上的根,构造了如下3个迭代函数:
(1)  ; (2)
; (2) 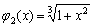 ; (3)
; (3) 
若已知x0 = 1.5与精确根邻近,试分别写出它们的迭代公式,并用局部收敛的近似替代判别方法分析收敛性,再取其中一种收敛的公式求出近似根(要求精确到小数点后2位).
解 (1) ,因为
,因为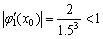 ,此迭代格式收敛;
,此迭代格式收敛;
(2) ,因为
,因为 ,所以此迭代格式发散;
,所以此迭代格式发散;
(3) ,因为
,因为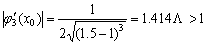 ,所以此迭代格式发散.
,所以此迭代格式发散.
用迭代格式(1)计算得
x1 = 1.444444444, x2 = 1.479289941,
x3 = 1.456976000, x4 = 1.471080583,
x5 = 1.462090536, x6 = 1.467790576,
x7 = 1.464164381, x8 = 1.466466355
12.填空题
(1) 对于方程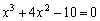 ,写出简单迭代法的两个迭代函数及其相应的迭代格式:
,写出简单迭代法的两个迭代函数及其相应的迭代格式:
迭代函数之一 ,迭代公式
,迭代公式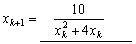
迭代函数之二 ,迭代公式
,迭代公式
(2) 简单迭代法的误差分析,有先验估计式
和事后估计式
(3) 要使简单迭代法的精度达到要求 ,实用中的一个简单易处理的方法,是根据不等式
,实用中的一个简单易处理的方法,是根据不等式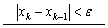 成立与否来判别是否终止迭代.
成立与否来判别是否终止迭代.
(4) 对于方程f(x) = 0的一个简单迭代公式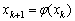 ,其收敛的一个充分条件是:当
,其收敛的一个充分条件是:当 时,φ (x)满足
时,φ (x)满足 ,若已知根的初始值x0在根x*邻近,则可将局部收敛的判别条件
,若已知根的初始值x0在根x*邻近,则可将局部收敛的判别条件 用
用 来替代.
来替代.
(5) 对于方程f (x) = 0的一个简单迭代公式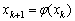 ,若其产生的序列{xk}收敛很慢,这时可令新的迭代函数为
,若其产生的序列{xk}收敛很慢,这时可令新的迭代函数为 ,要想得到收敛速度更快的迭代函数,k的最好取值是使
,要想得到收敛速度更快的迭代函数,k的最好取值是使 满足
满足 .由于方程的解x*未知,通常取
.由于方程的解x*未知,通常取 ,可得加速迭代公式
,可得加速迭代公式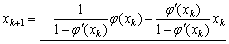
(6) 对迭代格式xk+1 = φ(xk),若φ(xk)满足
 ,而
,而
那么该格式收敛的阶数是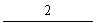
2.4 牛顿迭代法
13.用牛顿迭代法求方程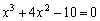 在[1, 2]上的根.
在[1, 2]上的根.
(1) 写出该方程的牛顿迭代公式.
解  ,
, 
牛顿迭代公式为 


(2) 取初值x0 =1.5,证明该方程的牛顿迭代公式收敛.
证明 f (1) = -5,f (2) = 41,f (1) f
(2) < 0
当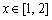 时
时  ,
,
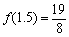 ,
, ,所以迭代格式收敛.
,所以迭代格式收敛.
(3) 迭代求出方程的近似根xk,要求精度: .
.
解 将x0 =1.5代入迭代公式得
x1 = 1.373333333,x2 = 1.365262015
x3 = 1.365230014,x4 = 1.365230013
由于x4满足 ,故近似根取作x4 = 1.365230013
,故近似根取作x4 = 1.365230013
14.选择题
如下说法中,不正确的是( C )
(A) 牛顿迭代法也是一种简单迭代法
(B) 牛顿迭代法也叫牛顿切线法
(C) 当x0充分接近x*时,弦截法比牛顿法收敛快
(D) 弦截法的优点是不需要计算导数值
15.填空题
(1) 对于方程f(x)
= 0,已知其根x*介于a,b之间,初值 .证明该方程的牛顿迭代公式收敛,需验证成立的条件为
.证明该方程的牛顿迭代公式收敛,需验证成立的条件为
① 
② 
③ 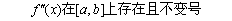
④ 
(2) 求解方程 的牛顿迭代公式为
的牛顿迭代公式为 
(3) 用牛顿法计算 的值,其迭代公式为
的值,其迭代公式为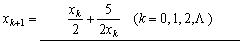
取x0 =
2,得 的各近似值:
的各近似值:
 ,
,  ,
, 
精确到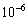 的近似值为 2.236067978
的近似值为 2.236067978
(4) 对于方程
其弦截法迭代公式为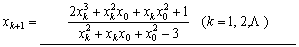
16.用牛顿迭代法求方程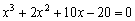 在x0 = 1.5附近的根.
在x0 = 1.5附近的根.
解 迭代格式为

将x0 =1.5代入迭代公式计算得
x1 = 1.373626373,x2 = 1.368814819,x3 = 1.368808107,x4 = 1.368808107
17.用快速弦截法求方程 在区间[1, 2]内的根,精确至5位有效数字.
在区间[1, 2]内的根,精确至5位有效数字.
解 取x0 = 1.4,x1 = 1.6,代人迭代公式
 ,
, 
代入计算得 f (x0) =-2.168, f (x1) = 1.176,x2 =1.52967;
f (x2) = 0.0692609, x3 = 1.51069;
f (x3) = -0.216464, x4 = 1.52417;
f (x4) = -0.0140970, x5 = 1.52511;
f (x5) =
0.000117173, x6 = 1.52510;
所以 .
.
3.2 线性方程组的直接解法
1.选择题
当n阶方阵A满足条件( A
)时,线性方程组Ax = b有唯一解.
(A) A非奇异 (B) R(A)
≠ 0
(C) R(A) < n (D) 以上都不对
2.填空题
(1) 如果一种算法在计算中舍入误差积累迅速增长,无法控制,造成结果失真,则称这一算法是数值不稳定的,反之是数值稳定的.高斯消去法是 数值不稳定 的算法
(2) 解线性方程组的直接法有消去法与列主元消去法,其中 列主元消去法 有利于控制误差的增长,这是因为它能有效克服“小”主元带来的 “大数吃小数” 现象,从而有效控制误差的增长
(3) 过三点(1, 1)、(2, -1)和(3, 1)的抛物线为
y = 2x2 - 8x + 7
(4) 用列主元高斯消去法,对方程组的增广矩阵作初等变换,当进行至

时,下一步所选主元为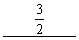
3.用高斯消去法求解方程组
 .
.
解 记B = (A, b),B称为增广矩阵,用对增广矩阵的初等行变换表示消元过程如下





回代得
x3 =8.4, x2 =2.6, x1 =-10.8
4.用列主元消去法求解方程组(计算结果保留到小数点后3位)
 .
.
解 
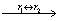





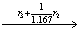

回代得
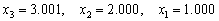 .
.
3.3 线性方程组的直接分解法
5.判断题
(1) 当矩阵A的各阶前主子式都不等于零时,可唯一地分解为一个单位下三角阵L和一个上三角阵U的乘积.
( √ )
(2) 若不计舍入误差,LU分解法是求解线性方程组的精确方法. (
√ )
(3) LU分解法中的U就是高斯消去法得到的上三角方程组的系数矩阵. (
√ )
6.用矩阵的LU分解法求解线性方程组Ax = b,其中
 ,
, 
解 对A做LU分解,先计算U的第一行及L的第一列
u11 =
a11 = 9, u12 =
a12 = 18, u13 =
a13 = 9, u14 =
a14 = -27
l21 = a21 / u11 = 2, l31= a31 /
u11 = 1, l41= a41 /
u11 = -3
然后计算U的第二行及L的第二列
u22 =
a22 - l21 u12 =
9, u23 =
a23- l21 u13 =
-18, u24 =
a24- l21 u14 =
9
l32 =
(a32 - l31 u12) /
u22 = -2, l42 = (a42- l41 u12) / u22 = 1
再计算U的第三行及L的第三列
u33 =
a33- l31 u13- l32 u23 =
81, u34 =
a34- l31 u14- l32 u24 =
54
l43 =
(a43- l41 u13- l42 u23) /
u33 = 
最后计算u44
u44 =
a44- l41 u14- l42 u24- l43 u34 =
9
因此

解方程组Ly = b,得
y = (1, 0, 15, 1)T
解方程组Ux = y,得

7.用LU紧凑格式分解法求解线性方程组Ax = b,其中
 ,
, 
解 对增广矩阵进行紧凑格式分解,有

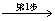

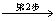


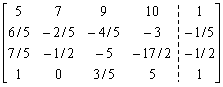
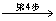

所以  ,
, ,
,
解方程组Ux = y,得
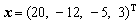
3.4 特殊线性方程组的解法
8.选择题
(1) 当矩阵A满足条件(
C )时,解方程组Ax = b的LU分解法就可用改进的平方根法(或称改进的乔累斯基分解法)来求解,从而减少计算量.
(A) A对称正定 (B) A的所有顺序主子式都大于零
(C) 选项(A)、(B)结合 (D) A非奇异
(2) 当方程组Ax = b的系数矩阵为三对角矩阵时,由对A的LU分解公式,可得到求解三对角方程组的( B
)
(A) 乔累斯基分解法 (B) 追赶法
(C) LDLT分解法 (D) 以上选项都不对
9.填空题:用改进的平方根法(或改进的乔累斯基分解法)求解线性方程组

对其增广矩阵进行如下的紧凑格式分解:

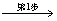





得到等价的三角形方程组为
 , 回代解得
, 回代解得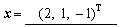
10.用追赶法求解方程组

解 求得
q1 = 2,q2
= 3/2,q3 = 4/3,q4
= 5/4,q5 = 6/5;
p2 = 1/2,p3 = 2/3,p4
= 3/4,p5 = 4/5
解方程组Ly = f,得
y = (1, -1/2, 1/3, -1/4, 6/5)T
解方程组Ux = y,得
x = (1, -1, 1, -1, 1)T.
3.5 向量与矩阵的范数
1.填空题
(1) 设x = (1, -1, 2)T,那么 ,
,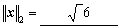 ,
,
(2)
设矩阵 ,那么
,那么 ,
,

(3) 矩阵 ,则A的条件数
,则A的条件数
(4) 已知A为n阶对称矩阵,且ρ(A) = 3,那么
(5) 线性方程组的性态是衡量方程组的解对扰动(误差)的敏感程度的,若较小的扰动带来解的较大变化,那么称方程组是病态的,否则称为良态的.一般如果系数矩阵A的条件数cond(A)
远远大于1 时,方程组是病态的.
(6) 对任一n维向量x =(x1, x2,…,xn)T,不同的范数,其值不同,但总满足下面关系式

2.判断题
(1) 对任何非奇异矩方阵A,都有cond
(A) ≥ 1. ( √ )
(2) 对任何非奇异矩方阵A的任一范数,都有ρ(A) ≥ ||A||. ( × )
(3) 若线性方程组的系数矩阵A的各元素间量级差异很大且无一定规律,或者某些行(列)近似线性相关,则方程组可能为病态的. ( √ )
(4) 方程组的性态是其固有性质,任何方法都不可能改变其病态程度. ( × )
3.设矩阵 ,求||A||p ( p = 1, 2, ∞)和ρ(A).
,求||A||p ( p = 1, 2, ∞)和ρ(A).
解 因为A为对称矩阵,因此
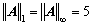
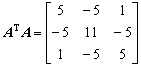 ,
,
λ1 = 1,λ2 =
4,λ3 = 16,ρ(ATA) = 16,因此
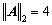
由于A为对称矩阵,所以

4.证明:对于矩阵A范数,如果 ,则
,则

证明

移项得

两边同时取范数得

移项得
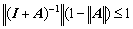
因为 ,从而有
,从而有

5.填空题
(1) 已知线性方程组Ax = b为
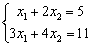
①
给右端项b一扰动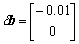 ,取无穷大范数,利用公式
,取无穷大范数,利用公式

估计解x的相对误差,求得
 ,
,  ,
, 


从而

②
给系数矩阵A一扰动 ,取无穷大范数,利用公式
,取无穷大范数,利用公式

估计解x的相对误差,求得
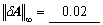
从而
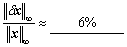
(2) 希尔伯特(Hilbert)矩阵(又称坡度阵)

是有名的病态阵,当n = 3时, ,且随着阶数的增大,条件数迅速增大.
,且随着阶数的增大,条件数迅速增大.
3.6 线性方程组的迭代解法
6.给定线性方程组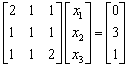
(1) 分别写出雅可比和高斯-塞德尔迭代格式,并判断它们的收敛性.
解 雅可比迭代格式为 
 ,
,  ,所以雅可比迭代格式发散.
,所以雅可比迭代格式发散.
高斯-塞德尔迭代格式为
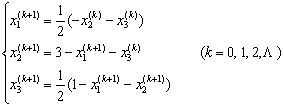
 ,
,
所以高斯-塞德尔迭代格式收敛.
(2) 取初值x (0) =
(0, 0, 0)T,用(2)中收敛的迭代格式求解(保留到小数点后4位).
解 (2)中赛德尔迭代格式收敛.取初值x(0)=(0,
0, 0)T,迭代计算得
x(1) =
(0.000 0, 3.000 0, -1.000 0)T,
x(2) = (-1.000 0, 5.000 0, -1.500 0)T,
x(3) = (-1.750 0, 6.250 0, -1.750 0)T,
x(4) = (-2.250 0, 7.000 0, -1.875 0)T,
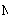
(精确解为x = (-3, 8, -2)T)
7.填空题
(1) 将方程组

中方程的顺序由“①-②-③”调整为 ③-①-② 能使雅可比和高斯-塞德尔迭代收敛.
(2) 用高斯-塞德尔迭代法求解线性方程组

那么迭代格式 收敛
.(填“收敛”或“不收敛”)
(3) 解线性方程组 的高斯-赛德尔迭代格式为
的高斯-赛德尔迭代格式为

8.判断题
(1) 对线性方程组Ax = b构造的雅可比、高斯-塞德尔和超松弛迭代格式的收敛性仅与方程组的系数矩阵A有关,而与迭代初值x (0)无关. ( √ )
(2) 高斯-塞德尔迭代格式一定比雅可比迭代格式收敛速度快. ( × )
(3) 若方阵A严格对角占优,则A非奇异.
( √ )
(4) 对收敛的迭代格式,在迭代计算的过程中,不怕中途出错. (
√ )
9.对方程组

用超松弛迭代(取ω = 1.1)求解,取初值x(0) = (0, 0, 0)T,并精确到小数点后3位.
解 ω = 1.1时迭代格式为

初值x(0) =
(0, 0, 0)T,迭代计算得
x(1) =
(0.550 0, 3.135 0, -1.025 7)T
x(2) =
(2.219 3, 3.057 4, -1.965 8)T

x(7) =
(2.000 0, 3.000 0, -1.000 0)T
4.2 拉格朗日插值
1.填空题
(1) 过点(0, 2)、(1, 1)、(2, 2)的不超过2次的多项式为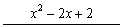
(2) 设xi (i = 0, 1, 2, …, n)为n+1个互异的插值节点,li (x)为相应的Lagrange插值基函数,则
(3) 设xi = i (i
= 0, 1, 2, …, n)为n+1个互异的插值节点,li(x)是相应的n次Lagrange插值基函数,则
(4) 设li(x)是对n+1个点xi (i = 0, 1, 2, …, n)进行Lagrange插值的基函数,则

(5) 如果记R(x)为过两点(x0, y0)、(x1, y1)的插值多项式P1(x)的余项,则R(x)的误差限为
(6) 多项式
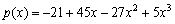 和
和 
都能插值下表
这是否违背插值多项式的唯一性? 否 (填“是”或“否”)
2.给定数据表
|
x
|
0
|
2
|
3
|
5
|
|
f (x)
|
1
|
-3
|
-4
|
2
|
用拉格朗日插值方法求出f (x)的不超过3次的插值多项式L3(x).
解 先构造基函数如下



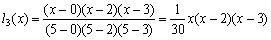
所以拉格朗日插值多项式为
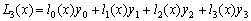


3.将下面计算过程补充完整
给定函数sinx的数值表如下
|
x
|
0.32
|
0.34
|
0.36
|
|
sinx
|
0.314567
|
0.333487
|
0.352274
|
用线性插值和抛物线插值计算sin0.3367的值,并利用插值余项给出计算结果的误差限.取
x0 = 0.32,y0 =
0.314567; x1 = 0.34,y1 =
0.333487; x2 = 0.36,y2 =
0.352274
(1) 线性插值:由于0.32<0.336 7<0.34,在区间[x0, x1]上进行插值,求得
 ,
, 
从而

由于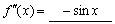 ,因而
,因而
 (ξ∈[0.32, 0.34] )
(ξ∈[0.32, 0.34] )

(2) 抛物线插值:求得  393.20875(x-0.34)(x-0.36)
393.20875(x-0.34)(x-0.36)
 -833.7175(x-0.32)(x-0.36) ,
-833.7175(x-0.32)(x-0.36) ,  440.3425(x-0.32)(x-0.34)
440.3425(x-0.32)(x-0.34)
从而

由于 ,因而
,因而
 (ξ∈[0.32, 0.36] )
(ξ∈[0.32, 0.36] )

4.已知多项式 通过下列点:
通过下列点:
|
x
|
-2
|
-1
|
0
|
1
|
2
|
3
|
|
p(x)
|
31
|
5
|
1
|
1
|
11
|
61
|
试构造一多项式q(x)且通过下列各点:
|
x
|
-2
|
-1
|
0
|
1
|
2
|
3
|
|
q(x)
|
31
|
5
|
1
|
1
|
11
|
1
|
解 设r(x) = p(x) - q(x),则r(x)满足
|
x
|
-2
|
-1
|
0
|
1
|
2
|
3
|
|
r(x)
|
0
|
0
|
0
|
0
|
0
|
60
|
由拉格朗日插值方法知

于是

4.3 差商与牛顿插值
5.填空题
(1) 设f (x)
= an x n +1(an ≠ 0),则
(2) 设f (x)
= x2+2x,则 ,
,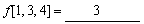
(3) 对函数表
|
x
|
-1
|
0
|
1
|
2
|
|
f (x)
|
1
|
-2
|
5
|
10
|
求得其各阶差商如下表
|
x
|
f (x)
|
一阶差商
|
二阶差商
|
三阶差商
|
|
|
-1
0
1
2
( 3 )
|
1
-2
5
10
( 25 )
|
-3
7
5
( 15 )
|
5
-1
( 5 )
|
-2
( 2 )
|
( 1 )
|
那么过这四个点的牛顿插值多项式为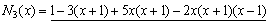
对新增节点x = 3,f (x) = 25,请完成上面的差商计算表;并写出过这五个节点的牛顿插值多项式
6.判断题
(1) 交换差商f [x0,
x1,…, xk]中的任意两个节点,差商的值改变符号.
( × )
(2) 若在原有数据上增加一组数据,则使用牛顿插值的插值多项式只增加一项,不必重复计算所有系数.
( √ )
(3) 对同一个插值问题,其牛顿插值多项式与拉格朗日多项式相同,且两种余项也相同.
( √ )
7.给定数据表
|
x
|
0
|
2
|
3
|
5
|
|
f (x)
|
1
|
-3
|
-4
|
2
|
(1) 求出f (x)的不超过3次的插值多项式.
解 计算均差表如下
|
x
|
f(x)
|
一阶均差
|
二阶均差
|
三阶均差
|
四阶均差
|
|
0
|
1
|
|
|
|
|
|
2
|
-3
|
-2
|
|
|
|
|
3
|
-4
|
-1
|
1/3
|
|
|
|
5
|
2
|
3
|
4/3
|
1/5
|
|
|
4
|
-1
|
3
|
0
|
-2/3
|
-13/60
|
所以牛顿插值多项式为
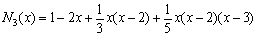

(2) 若增加一组数据 (4, -1),求f (x)的不超过4次的插值多项式,并求f (1.5)的近似值.
解 若增加一组数(4, -1),则在上述均差表增加一行一列(见上表双下划线).
 .
.
f (1.5)≈N4(1.5)
= -1.718861.
8.完成下面计算过程
已知单调连续函数y = f (x)的如下数值表
|
x
|
0
|
0.2
|
0.4
|
0.6
|
0.8
|
|
f (x)
|
0.1995
|
0.3965
|
0.5881
|
0.7721
|
0.9461
|
用反插值插值方法求方程f (x) = 0.4500在(0.00, 1.80)内的根的近似值.
将y作为自变量,采用牛顿插值,完成下面均差表
|
f(xi)
|
xi
|
一阶均差
|
二阶均差
|
三阶均差
|
四阶均差
|
|
0.199 5
0.396 5
0.588 1
0.772 1
0.946 1
|
0
0.2
0.4
0.6
0.8
|
( 0.015228 )
( 1.043841 )
( 1.086957 )
( 1.149425 )
|
( 0.073631 )
( 0.114792 )
( 0.174492 )
|
( 0.071884 )
( 0.108624 )
|
( 0.049209 )
|
从而得到4次插值多项式为
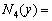 1.015228 ×(y - 0.1995)+
0.073631 ×(y - 0.1995)(y - 0.3965)
1.015228 ×(y - 0.1995)+
0.073631 ×(y - 0.1995)(y - 0.3965)
+
0.071884 ×(y - 0.1995)(y - 0.3965)(y - 0.5881)
+
0.049209 ×(y - 0.1995)(y - 0.3965)(y -
0.5881 )(y - 0.7721)
于是方程f (x) = 0.4500的根为

4.5 分段低次插值
9.对函数 在区间[1, 2]上作等距分段线性插值,怎样选择步长h,才能使插值误差小于
在区间[1, 2]上作等距分段线性插值,怎样选择步长h,才能使插值误差小于 ?
?
解  ,
, 
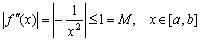
由 得
得
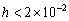
5.2 牛顿-柯特斯求积公式
1.填空题
(1) 牛顿-柯特斯公式 的系数和
的系数和
(2) 在牛顿-柯特斯求积公式

中,当系数 有负值时,公式的稳定性不能保证,所以实际应用中,当
有负值时,公式的稳定性不能保证,所以实际应用中,当 时,牛顿-柯特斯公式不使用.
时,牛顿-柯特斯公式不使用.
(3) 计算积分 ,取4位有效数字,用梯形公式求得的近似值为
,取4位有效数字,用梯形公式求得的近似值为
用辛普森公式求得的近似值为
2.判断题
(1) 牛顿-柯特斯求积公式的系数和 将随着点数的增加而增大. ( × )
将随着点数的增加而增大. ( × )
(2) 牛顿-柯特斯公式计算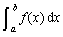 时,节点取得越多,则精度越高. ( × )
时,节点取得越多,则精度越高. ( × )
(3) 用辛普森求积公式,其误差为

( √ )
(4) 用梯形求积公式,其误差为
 ( √ )
( √ )
3.试用n = 1,2,3的牛顿-柯特斯公式计算积分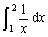 .
.
解 当n = 1时, ,从而有
,从而有
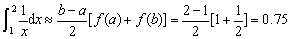
当n = 2时, ,
,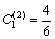 ,从而有
,从而有
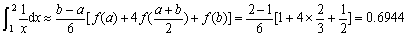
当n =3时, ,
, ,从而有
,从而有
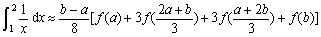

5.3 复合求积公式
4.填空题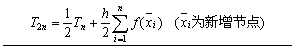
(1) 用变步长梯形求积法的计算过程中,要判断计算结果的精度是否满足 ,由
,由 得出的近似判别条件是
得出的近似判别条件是
(2) 变步长梯形求积公式中,设n等分时的步长为h,这时的积分值为Tn,步长减半后的积分值为T2n,那么Tn和T2n之间的关系式为
5.选择题
(1) 当 在区间[a, b]上具六阶连续导数,
在区间[a, b]上具六阶连续导数, 充分小时,分别用复合梯型求积公式Tn、复合辛普森求积公式Sn和复合柯特斯求积公式Cn,计算定积分
充分小时,分别用复合梯型求积公式Tn、复合辛普森求积公式Sn和复合柯特斯求积公式Cn,计算定积分 ,其精确度从高到低,依次是( A )
,其精确度从高到低,依次是( A )
(A) Tn,Sn,Cn (B) Tn,Cn,Sn
(C) Sn,Tn,Cn (D) Cn,Sn,Tn
(2) 用复合梯形公式Tn计算定积分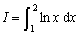 ,要使误差
,要使误差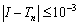 ,n应该不小于( B )
,n应该不小于( B )
(A) 5
(B) 10 (C)
20 (D) 50
(3) 用复合辛普森公式Sn计算定积分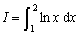 ,要使误差
,要使误差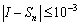 ,
,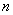 应该不小于( B ).
应该不小于( B ).
(A) 1
(B) 2 (C)
5 (D) 10
(4) 用复合柯特斯公式Cn计算定积分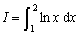 ,要使误差
,要使误差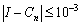 ,
,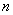 应该不小于( A ).
应该不小于( A ).
(A) 1
(B) 2 (C)
3 (D) 40
6.用n = 4的复合辛普森公式S4积分 .
.
解 
=3.14159250
7.用变步长梯形求积法计算积分 ,要求精确至3位有效数字.
,要求精确至3位有效数字.
(提示:先换元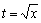 化为常义积分后再计算)
化为常义积分后再计算)
解 x = 0为被积函数的瑕点,作变换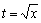 ,积分化为
,积分化为 .由复化梯形公式
.由复化梯形公式
 (这里
(这里 )
)
计算可得: T1=1.5,T2=1.55,T4=1.5656,T8=1.5695
至此,有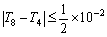 ,所以
,所以 .
.
5.4 龙贝格求积方法
8.填空题
(1) 辛普森求积公式经过龙贝格加速得到 的牛顿-柯特斯公式.
的牛顿-柯特斯公式.
(2) 龙贝格求积方法需要用到的4个公式分别为


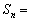




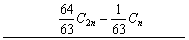
(3) 龙贝格求积方法的三个加速公式分别是根据梯形公式、辛普森公式和柯特斯公式的 导出的.
导出的.
(4) 用龙贝格求积法求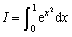 的近似值,求得
的近似值,求得
k = 1时: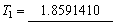
k = 2时: ,
, ,
,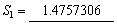
k = 3时: ,
, ,
, 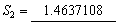 ,
,
k = 4时: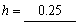 ,
, ,
, ;
;
9.判断题
(1) 对n = 4的牛顿-柯特斯求积公式作龙贝格加速,所得公式仍属牛顿-柯特斯求积公式序列.
( × )
(2) 龙贝格求积公式是一种要将积分区间等分的求积公式. ( √
)
10.用龙贝格算法计算积分 ,要求误差不超过
,要求误差不超过 (其准确值为π).
(其准确值为π).
解  ,
,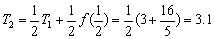
 ,
, 
 ,
, 

 ,
, 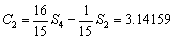


 ,
,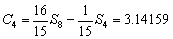 ,
,
由于|R2-R1| ≤ 0.00001,已精确到小数点后5位,故可取  .
.
11.填空题
(1) 由函数在一些离散点上的 来推算出函数在某些点处的导数近似值,这类问题称为数值微分.
来推算出函数在某些点处的导数近似值,这类问题称为数值微分.
(2) 中心差分公式

的截断误差为
(3) 二阶导数 的中心差分公式为
的中心差分公式为

其截断误差为
(4) 已知 ,取步长h = 0.01,
,取步长h = 0.01,
由向前差商公式得 
由向后差商公式得 
由中心差商公式得 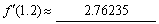
12.判断题
(1) 当插值多项式 收敛于
收敛于 时,不能保证
时,不能保证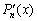 一定收敛于
一定收敛于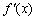 . ( √ )
. ( √ )
(2) 用差商公式近似计算函数的导数值,步长越小,则误差越小.
(
× )
(3) 用两点公式求得的一阶导数在x0、x1处的值完全相同,误差也完全相同. ( × )
13.已知以下数据
|
x
|
0.01
|
0.02
|
0.03
|
0.04
|
|
f (x)
|
0.0121
|
0.0124
|
0.0129
|
0.0139
|
若取h = 0.01,用中心差分公式计算函数在0.02,0.03处的一阶导数及在0.02处的二阶导数.
解 由中心差分公式,有




6.2 欧拉法和改进的欧拉法
1.填空题
(1) 对初值问题

若函数f ( x,
y )满足条件 ,则解y = y ( x
)存在且唯一.
,则解y = y ( x
)存在且唯一.
(2) 在区间[0, 1]上用欧拉方法求解初值问题

取步长h = 0.1,其差分格式为
(3)
初值问题的梯形公式

是 阶方法,是
阶方法,是 式的方法.(填“显式”或“隐式”)
式的方法.(填“显式”或“隐式”)
(4) 对于微分方程初值问题

的差分方法,如果当h→0时,其整体阶段误差ei →0时,则该方法是 收敛 的,欧拉方法是 收敛 的方法.(填“收敛”或“不收敛”)
(5) 改进的欧拉方法的整体截断误差为O(h2),局部截断误差为
2.用欧拉公式计算初值问题
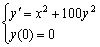
的解函数y = y (x)在x = 0.1,0.2,0.3处的近似值(保留4位小数).
解 由显式欧拉公式有

计算可得 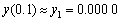

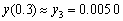
3.完成下面计算过程
用改进的欧拉公式求初值问题

的数值解(保留6位小数).
取h = 0.1,由于改进的欧拉公式为

因此该问题的计算格式为

计算结果填入下表
|
n
|
xn
|
yn
|
yp
|
yc
|
|
0
|
0
|
0
|
0
|
0.1
|
|
1
|
0.1
|
0.05
|
0.145
|
0.221
|
|
2
|
0.2
|
0.183
|
0.346 4
|
0.379 08
|
|
3
|
0.3
|
0.362 742
|
0.553 918
|
0.541 173
|
|
4
|
0.4
|
0.547 545
|
0.728 527
|
0.683 282
|
|
5
|
0.5
|
0.705 904
|
0.852 952
|
0.794 133
|
4.试导出求解初值问题

的隐式欧拉格式

并估计其局部截断误差.
解 对 两端同时积分,有
两端同时积分,有

并对右端用右矩形方法近似计算,得
代入上式,并用yi+1,yi代替y ( xi+1 ),y ( xi ),即得隐式欧拉格式

再求它的局部截断误差.在yi = y ( xi )的条件下,有
而按泰勒公式,有

因此
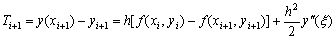
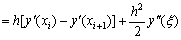

所以该格式为一阶方法.
6.3 龙格-库塔方法
5.选择题
(1) 求解常微分初值问题的中点格式
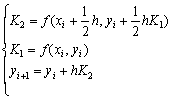
的局部截断误差为( C
)
(A) O(h) (B)
O(h2)
(C) O(h 3) (D)
O(h4)
(2) 求解常微分方程初值问题的数值公式

是( B
)
(A)
单步二阶法
(B) 多步二阶法
(C)
单步一阶法 (D)
多步一阶法
(3) 经典的四阶龙格-库塔(Runge-Kutta)方法的局部截断误差为( D
)
(A) O(h2) (B) O(h3)
(C) O(h4) (D) O(h5)
6.填空题
(1) 龙格-库塔方法的基本思想是:通过对不同点上f (x, y)的函数值的 线性组合 来构造近似公式的,若有m个点,则其局部截断误差为
(2) 用四阶经典龙格-库塔方法求解初值问题
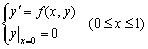
时,取h = 0.1,得y(1)的近似值为0.42671,而取h = 0.05,得y(1)的近似值为0.43382,若不考虑舍入误差,则y(1)的更好的近似值是
7.取步长h = 0.4,写出用经典四阶龙格-库塔方法求解初值问题
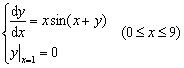
的计算公式.
解
 ,
,

8.填空题
(1) 用经典的3阶龙格-库塔方法解初值问题
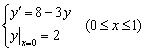
取步长h = 0.2,则 ,
,
(2) 用3阶库塔格式

求解初值问题

取步长h = 0.1,该方程的库塔计算格式为
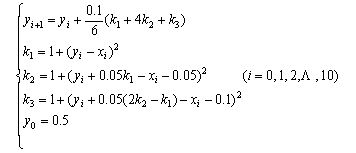
取5位小数,计算y (0.1)的近似值,将初值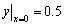 代入得
代入得
 ,
, ,
,
因此
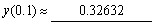
9.取h = 0.4,用经典四阶龙格-库塔方法求初值问题

的数值解,并与准确解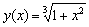 进行比较.
进行比较.
解  ,取h = 0.4,x0 = 0,x1 = 0.4,x2 = 0.8,x3 = 1.2,则有
,取h = 0.4,x0 = 0,x1 = 0.4,x2 = 0.8,x3 = 1.2,则有

计算结果如下:
|
xi
|
yi
|
K1
|
K2
|
K3
|
K4
|
y(xi)
|
|y(xi)-yi|
|
|
0
|
1
|
0
|
0.133333
|
0.126497
|
0.241599
|
1
|
0
|
|
0.4
|
1.050751
|
0.241519
|
0.3311616
|
0.320604
|
0.383687
|
1.050718
|
3.34×10-5
|
|
0.8
|
1.179332
|
0.383466
|
0.422583
|
0.417368
|
0.4413687
|
1.179274
|
5.83×10-5
|
|
1.2
|
1.346316
|
|
|
|
|
1.346263
|
5.29×10-5
|
![]()
![]() 的有效位数是
的有效位数是![]()
![]() 的有效位数是
的有效位数是![]()
![]()
![]() ,则x*的有效位数至少是
,则x*的有效位数至少是 ![]()
![]() 个数.
个数.![]() 表示
表示![]() 充分大,
充分大,![]() 表示x充分接近0).
表示x充分接近0).![]() ,
,![]()
![]()
![]() ,
, ![]()

![]() ,所以
,所以![]()
![]()
![]()
![]() ,说明ac + b
= 14.2265有3位有效数字,ac + b ≈ 14.2
,说明ac + b
= 14.2265有3位有效数字,ac + b ≈ 14.2![]()
![]() ,可按以下两种顺序进行:
,可按以下两种顺序进行:![]() 的值,采用秦九韶算法要做 n 次乘法运算,而直接计算需要作
的值,采用秦九韶算法要做 n 次乘法运算,而直接计算需要作![]() 次乘法运算.
次乘法运算.![]() 的值.
的值.![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,分别计算
,分别计算![]() 和
和![]() ,并求各结果与精确结果的绝对误差.
,并求各结果与精确结果的绝对误差.![]()
![]()
![]()
![]()
![]()
![]()
![]() 比较,二者的绝对误差分别为
比较,二者的绝对误差分别为![]()
![]()
![]()
![]() ,试求函数
,试求函数![]() 的相对误差限.
的相对误差限.![]() ,
,![]() ,
,![]() ,
,![]() 的相对误差限为
的相对误差限为![]()
![]() ,则方程在[a, b]上有且仅有一个实根x*
,则方程在[a, b]上有且仅有一个实根x*![]() ,所以要使
,所以要使![]() 成立,只需
成立,只需![]() 即可
即可![]() ,至少要二分区间
,至少要二分区间![]() 次
次![]() 在[1, 2]内的根,要求精确到小数点后第二位,即误差不超过
在[1, 2]内的根,要求精确到小数点后第二位,即误差不超过![]() .
.![]() ,由
,由![]() ,得k+1≥7,所以迭代7次即可.计算结果如下表:
,得k+1≥7,所以迭代7次即可.计算结果如下表:![]() 在区间[1, 2]上的根,构造了如下3个迭代函数:
在区间[1, 2]上的根,构造了如下3个迭代函数:![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]()
![]() ,因为
,因为![]() ,此迭代格式收敛;
,此迭代格式收敛;![]() ,因为
,因为![]() ,所以此迭代格式发散;
,所以此迭代格式发散;![]() ,因为
,因为![]() ,所以此迭代格式发散.
,所以此迭代格式发散.![]() ,写出简单迭代法的两个迭代函数及其相应的迭代格式:
,写出简单迭代法的两个迭代函数及其相应的迭代格式:![]() ,迭代公式
,迭代公式![]()
![]() ,迭代公式
,迭代公式![]()
![]()
![]()
![]() ,实用中的一个简单易处理的方法,是根据不等式
,实用中的一个简单易处理的方法,是根据不等式![]() 成立与否来判别是否终止迭代.
成立与否来判别是否终止迭代.![]() ,其收敛的一个充分条件是:当
,其收敛的一个充分条件是:当![]() 时,φ (x)满足
时,φ (x)满足![]() ,若已知根的初始值x0在根x*邻近,则可将局部收敛的判别条件
,若已知根的初始值x0在根x*邻近,则可将局部收敛的判别条件![]() 用
用![]() 来替代.
来替代.![]() ,若其产生的序列{xk}收敛很慢,这时可令新的迭代函数为
,若其产生的序列{xk}收敛很慢,这时可令新的迭代函数为![]() ,要想得到收敛速度更快的迭代函数,k的最好取值是使
,要想得到收敛速度更快的迭代函数,k的最好取值是使![]() 满足
满足![]() .由于方程的解x*未知,通常取
.由于方程的解x*未知,通常取![]() ,可得加速迭代公式
,可得加速迭代公式![]()
![]() ,而
,而![]()
![]() 在[1, 2]上的根.
在[1, 2]上的根.![]() ,
, ![]()
![]()
![]()
![]()
![]() 时
时 ![]() ,
,![]()
![]() ,
,![]() ,所以迭代格式收敛.
,所以迭代格式收敛.![]() .
.![]() ,故近似根取作x4 = 1.365230013
,故近似根取作x4 = 1.365230013![]() .证明该方程的牛顿迭代公式收敛,需验证成立的条件为
.证明该方程的牛顿迭代公式收敛,需验证成立的条件为![]()
![]()
![]()
![]()
![]() 的牛顿迭代公式为
的牛顿迭代公式为 ![]()
![]() 的值,其迭代公式为
的值,其迭代公式为![]()
![]() 的各近似值:
的各近似值:![]() ,
, ![]() ,
, ![]()
![]() 的近似值为 2.236067978
的近似值为 2.236067978 ![]()
![]()
![]() 在x0 = 1.5附近的根.
在x0 = 1.5附近的根.![]()
![]() 在区间[1, 2]内的根,精确至5位有效数字.
在区间[1, 2]内的根,精确至5位有效数字.![]() ,
, ![]()
![]() .
.