2000-2001学年 参考答案
1.(10分)
解: (1分)
(1分) (2分)
(2分) (2分)
(2分)
 (2分)回代解得
(2分)回代解得![]() ,
,![]() ,
,![]() (1分)
(1分)
2.(10分)解:牛顿迭代公式为:![]() (1分);三种变形分别为:简单牛顿法
(1分);三种变形分别为:简单牛顿法![]() (1分)牛顿下山法
(1分)牛顿下山法![]() (1分)
(1分)
割线法![]() (1分)
(1分)
利用牛顿迭代法求解:![]() 代入
代入
![]() (1分),
(1分),![]() (1分)
(1分)
![]() (1分),
(1分),![]() (1分)
(1分)
∴![]() (2分)
(2分)
3.(22分)解:![]() (1分)
(1分)
![]()
![]()
(2分)
![]()
![]()
(2分)
![]()
![]()
(2分)
![]()
![]()
(2分)
![]() (1分)
(1分)
![]() (1分)
(1分)
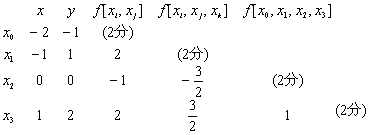
![]() (2分)
(2分)
![]() (1分)
(1分)
4.(10分)解:![]() (2分)
(2分)
1)取h=0.01时,![]() (4分)
(4分)
2)取h=0.02时,![]() (4分)
(4分)
5.(20分)解:其Jacobi迭代格式为: (5分)
(5分)
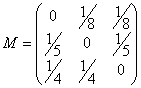 (2分)
(2分) ![]() <1 (2分) ∴收敛 (1分)
<1 (2分) ∴收敛 (1分)
解:其Seidle迭代格式为: (5分)
(5分)
取![]() T;
T;![]() ,
,![]() ,
,![]() )(3分)
)(3分)
∴||![]() -
-![]() ||=
||=![]() (2分)
(2分)
6.(15分)解:![]() (2分)
(2分)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() (9个每个1分)
(9个每个1分)
![]()
![]() (4分)
(4分)
7.(15分)解:改进的欧拉公式: (3分)
(3分)
∴ (2分)
(2分)
∴x0=0, y0=0,yp=0.2 (2分)
x1=0.2,y1=0.26,yp=0.604 (3分)
x2=0.4,y2=0.5928,yp=1.10991 (3分)
x3=0.6,y3=1.23344 (2分)
2001~2002学年 参考答案
1.(10分)解:1)Cond∞(A)=![]() 1分
1分
![]() ∴
∴![]() 2分
2分
![]() 1分 ∴
1分 ∴![]() 1分
1分
∴Cond∞(A)=17×17=289 2分
2). 3分
3分
2.(14分)解:seidel迭代格式
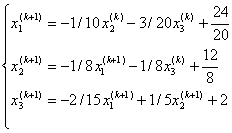 5分
5分
![]() ,
,![]() (3分),
(3分),![]() (3分)
(3分)
∴![]() =0.4485 3分
=0.4485 3分
3.(4分)解:构造一种迭代格式![]()
![]() 3分 取
3分 取![]()
![]() 1分
1分 ![]() 1分
1分 ![]() 1分
1分
![]() 1分
1分 ![]() 1分
1分 ![]() 1分
1分
![]() 1分
1分 ![]() 1分
1分 ![]() 1分
1分 ![]() 1分
1分 ![]() 1分
1分 ![]() 1分
1分
∴ ![]()
4.(17分)解:
|
|
|
|
|
|
0 -1 1 |
1(2分) 2 3 |
-1 (2分) 1/2 |
3/2 (2分) |
![]() 1分
1分
∴![]() 2分
2分
N2(1.5)=5.125 2分
再增加一对(2,0),补充差值,![]() 1分
1分
![]() 1分
1分
![]() 2分
2分
![]() 2分
2分
5.(10分)解:
![]() 3分
3分
![]() 1分
1分 ![]() 1分
1分
![]() 1分
1分
![]() 4分
4分
6.(18分)解:改进的Euler公式为
 (3分)
(3分)
![]()
![]()
![]() 1分
1分
![]()
![]()
![]() 3分
3分
![]()
![]()
![]() 3分
3分
![]()
![]()
![]() 3分
3分
![]()
![]()
![]() 3分
3分
![]()
![]()
∴![]() 2分
2分
7.(15分)解:设![]() ∴
∴![]() 5分
5分
Euler公式  5分
5分
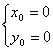

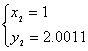
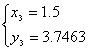
 1分
1分
四对全对再加1分
2002~2003学年 参考答案
1.(10分)解:设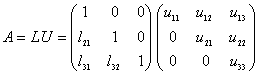 (1分)
(1分)
 (4分)LUX=b
(4分)LUX=b
其中设UX=y,则Ly=b![]()
 (2分)
(2分)
∴y=(2,-1,1)T UX=y  (2分)
(2分)
∴x=(0,-2,1)T (1分)
2.(10分)解:牛顿迭代法公式![]() (1分)
(1分)
![]() ,
,![]() (1分)
(1分)
Newton迭代公式:
∴![]() (3分)
(3分)
x0=2代入x1=1.870967742(1分)x2=1.855780702(1分)x3=1.855584561(1分)
x≈x3=1.85558(2分)
3.(20分)解:(1)L3(x)=lo(x)yo+l1(x)y1+l2(x)y2+l3(x)y3 (1分)
![]()
得出![]() (2分)
(2分)![]() (2分)
(2分)
![]() (2分)
(2分)![]() (2分)
(2分)
∴![]()
(1分)
(2)![]() (1分)
(1分)
![]() (2分)
(2分) ![]() (2分)
(2分)
 (2分),
(2分),![]() (2分)
(2分)
∴![]() (1分)
(1分)
4.(10分)解:中心差分公式![]() (2分)
(2分)
取h=0.3时,![]() (4分)
(4分)
取h=0.1时,![]() (4分)
(4分)
5.(20分)
(1)解:其Jacobi迭代格式为:
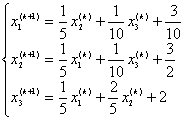 (5分)
(5分)  (6分)
(6分)
![]() <1 (2分)
<1 (2分)
∴收敛 (1分)
(2)解:其Seidle迭代格式为:
 (5分)
(5分)
![]() T
T
![]() T (2分)
T (2分)
![]() T (2分)
T (2分)
![]() T (1分)
T (1分)
6.(15分)
解:![]() (2分)
(2分)
![]()
![]() (3分)
(3分)
![]()
![]() (3分)
(3分)
f(0)=1,f(0.1)=0.9090,f(0.2)=.08333,f(0.3)=0.7692,f(0.4)=0.7142,
f(0.5)=0.6667,f(0.6)=0.625 (7分)
7.(15分)解:改进的欧拉公式: (2分)
(2分)
初值x0=0,y0=1  (2分)
(2分)
x0=0, y0=1,yp=1.1 (3分)
x1=0.1,y1=1.1+0.05[1+1.2]=1+0.11=1.11 yp=1.231 (3分)
x2=0.2,y2=1.24205 yp=1.38625 (3分)
x3=0.3,y3=1.39846525 (2分)
2003~2004学年
考试答案
1.(10分)
解: (1分)
(1分)

![]() (1分)
(1分) (2分)回代解得
(2分)回代解得![]() (1分)
(1分)
2.(10分)解:牛顿迭代法公式![]() (1分)
(1分)![]() (1分)
(1分)
故Newton迭代公式为 ![]() (3分)
(3分)
代入初值得 ![]() (1分)
(1分)![]() (1分)
(1分)![]() (1分)
(1分)![]() (1分)
(1分) ![]() (1分)。
(1分)。
3.(10分)解:![]() (1分)
(1分)
![]() (3分)
(3分)
![]() (3分)=
(3分)=![]() (2分)
(2分) ![]() (1分)
(1分)
|
|
|
|
1 |
0
2 2
4
10 2 12
10
(2分)
30
(2分) 42
(2分) |
|
2 |
|
|
3 |
|
|
4 |
![]() (3分)
(3分)
![]() (1分)
(1分)
4.(10分)解:中心差分公式 ![]() (1分)
(1分)
⑴ 取![]() 时,
时,![]() (3分)
(3分)
⑵ 取![]() 时,
时,![]() (3分)
(3分)
⑶ 取![]() 时,
时,![]() (3分)
(3分)
5.(20分)解:其Jacobi迭代格式为:
![]()
(4分) 此线性方程组的系数矩阵 严格对角占优 (3分),故Jacobi和Seidle迭代法均收敛(1分)
严格对角占优 (3分),故Jacobi和Seidle迭代法均收敛(1分)
(或迭代矩阵 (1分)
(1分) ![]() (2分) 所以收敛 (1分))
(2分) 所以收敛 (1分))
其Seidel迭代格式为:
![]() … (6分)
… (6分)
取![]() ,
,![]() (2分)
(2分) ![]() (2分)
(2分)
![]() (2分)
(2分)
6.(15分)解:![]() (2分)
(2分)
![]()
![]()
(3分) ![]() (2分)
(2分)
![]() (2分)
(2分)
![]()
(4分) ![]() (2分)
(2分)
7.(15分)解:改进的欧拉公式: (2分)
(2分)
初值 ![]()
 (2分)
(2分)
![]() (2分)
(2分)
![]()
![]() (3分)
(3分)
![]() ,
, ![]() (3分)
(3分)
![]() (3分)
(3分)
2005~2006学年 考试答案
一.(10分)解: (1分)
(1分)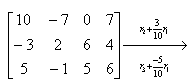 (1分)
(1分)
 (4分)
(4分)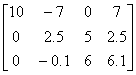
![]() (1分)
(1分)  (2分)
(2分)
回代解得![]() (1分).
(1分).
二.(10分)解:牛顿迭代公式为:![]() (3分).
(3分).
将f (x)代入得![]()
![]() (1分),
(1分),
![]() ,
,![]() (1分),
(1分),![]() (1分),
(1分),
![]() (1分),
(1分),![]() (1分),
(1分),
∴![]() .(2分)
.(2分)
三.(20分)解:Seidel迭代格式
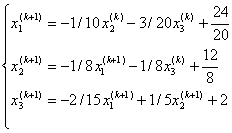 (5分)
(5分)
![]() ,
,![]() (3分),
(3分),![]() (3分)
(3分)
∴![]() =0.4485.(4分)因为系数矩阵严格对角占优,故该格式是收敛的.(5分)
=0.4485.(4分)因为系数矩阵严格对角占优,故该格式是收敛的.(5分)
四.(20分)解:(1)
|
|
|
|
|
|
0 -1 1 |
1 2 3 |
-1 1/2 |
3/2 |
(2分)
(2分)
(2分)
![]() (1分)
(1分)
∴![]() (1分)
(1分)
N2(1.5)=5.125. (1分)
(2)再增加一对数据(2,0),补充差值
![]() ,
,![]() ,
,![]() .(3分)
.(3分)
![]() (1分)
(1分)
(3) ![]() (1分)
(1分)
(4分)

![]() .(1分)
.(1分)
二者都是同一个多项式,只是构造过程不一样.(1分)
五.(10分)解:![]() (2分)
(2分)
取h = 0.01时,![]() (4分)
(4分)
取h = 0.02时,![]() (4分)
(4分)
六.(15分)解:
![]() (2分)
(2分)
![]()
![]() (3分)
(3分)
![]()
![]() (3分)
(3分)
f(0)=1,f(0.1)=0.9090,f(0.2)=.08333,f(0.3)=0.7692,f(0.4)=0.7142,
f(0.5)=0.6667,f(0.6)=0.625 (7分)
七.(15分)解:设![]() ∴
∴![]() (5分)
(5分)
Euler公式  (5分)
(5分)
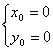
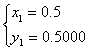
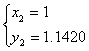
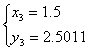
 .(5分)
.(5分)
2004~2005学年清考 参考答案
一.(15分)1 2;3 1 0; 4 70; 5 收敛.
2![]() 或
或![]() 或
或![]() 或
或![]() ;
;
二.(10分)
解: 1分~
1分~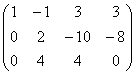 2分~
2分~ 2分
2分
∴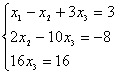 3分 ∴
3分 ∴![]() 2分
2分
三.(10分)解:![]() 2分
2分
∵![]() f(0)=2 (2分) f(1)=0.9092 (2分) f(1/2)=0.8414 (2分)
f(0)=2 (2分) f(1)=0.9092 (2分) f(1/2)=0.8414 (2分)
∴![]() =
=![]()
四.(15分)解:![]() 迭代格式
迭代格式 ![]() 2分
2分
![]() (2分)
(2分) ![]() (2分)
(2分) ![]() (2分)
(2分)
![]() (2分)
(2分) ![]() (2分)
(2分) ![]() (2分)
(2分)
∴![]() (1分)
(1分)
五.(20分)解:![]() (4分)
(4分)
![]() (3分)
(3分)
![]() (3分)=
(3分)=![]() (2分)
(2分)
![]() (1分)
(1分)
|
x |
y
|
|
1 |
0
2 2
4
10
2 12
10
(2分) 30
(2分) 42
(2分) |
|
2 |
|
|
3 |
|
|
4 |
![]() (3分)
(3分)
![]() (1分)
(1分)
六.(8分)解:欧拉公式为  (3分)
(3分)
改进的欧拉公式为 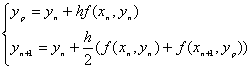 (3分)
(3分)
截断误差为分别为O(h)及O(h2),改进欧拉法比欧拉法的截断误差提高了一阶. (2分)
七.(10分)解:![]() (2分)
(2分)
取h = 0.01时,![]() (4分)
(4分)
取h = 0.02时,![]() (4分)
(4分)
2006-2007学年 参考答案
1.(10分)
解: (1分)
(1分)

![]() (1分)
(1分) (2分)回代解得
(2分)回代解得![]() (1分)
(1分)
2.(10分)解:牛顿迭代法公式![]() (2分)
(2分)
![]() ,
,![]() (2分)
(2分)
Newton迭代公式:
∴![]() (3分)
(3分)
x0=2代入x1=1.870967742(1分) x2=1.855780702(1分)
![]() (1分)
(1分)
3.(20分)解:
|
|
|
|
|
|
0 -1 1 |
1(2分) 2 3 |
-1 (2分) 1/2 |
3/2 (2分) |
![]() (2分)
(2分)
∴![]() (2分)
(2分)
N2(1.5)=5.125 (2分)
再增加一对(2,0),补充差值,![]() (2分)
(2分)
![]() (2分)
(2分)
![]() (2分)
(2分)
![]() (2分)
(2分)
4.(10分)解:![]() (2分)
(2分)
1)取h=0.01时,![]() (4分)
(4分)
2)取h=0.02时,![]() (4分)
(4分)
5.(20分)解:其Jacobi迭代格式为: (5分)
(5分)
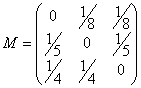 (2分)
(2分) ![]() <1 (2分) ∴收敛 (1分)
<1 (2分) ∴收敛 (1分)
解:其Seidel迭代格式为: (5分)
(5分)
取![]() T;
T;![]() ,
,![]() ,
,![]() )(3分)
)(3分)
∴||![]() -
-![]() ||=
||=![]() (2分)
(2分)
6.(15分)解:![]() (2分)
(2分)
![]()
![]()
(3分) ![]() (2分)
(2分)
![]() (2分)
(2分)
![]()
(4分) ![]() (2分)
(2分)
7.(15分)解:改进的欧拉公式: (4分)
(4分)
初值 ![]()
 (3分)
(3分)
![]() (2分)
(2分)
![]()
![]() (3分)
(3分)
![]() (3分)
(3分)
2007~2008学年 参考答案
一、单项选择题与填空题(![]() )
)
1.近似数![]() 关于真值
关于真值![]() 有效数字为( B ).
有效数字为( B ).
(A) 1位 (B) 2位 (C) 3位 (D) 4位
2.用对分法求方程![]() 在区间
在区间![]() 上的近似值,使误差不超过
上的近似值,使误差不超过![]() ,则至少对分( C ).
,则至少对分( C ).
(A) 3次 (B) 4次 (C) 5次 (D) 6次
3.已知![]() .取
.取![]() ,用三点公式计算
,用三点公式计算![]() 14.8865
14.8865
4.近似计算积分![]() 的抛物线求积公式
的抛物线求积公式![]()
5.设![]() 则
则![]() 0 .
0 .
二.(12分)用![]() 分解法解方程组
分解法解方程组

解:  (6分)
(6分)
 (3分)
(3分)
 (3分)
(3分)
三.(![]() )
)
1.利用牛顿迭代法迭代三次求![]() 的近似值
的近似值
解:1. 设![]() ,则求
,则求![]() 的正根就是求
的正根就是求![]() .(2分)由
.(2分)由![]() 知在
知在![]() 内方程有根.再由
内方程有根.再由![]()
![]() 知,可取
知,可取![]() ,(2分) 由牛顿法
,(2分) 由牛顿法![]() 得
得![]() ,
,![]() .所以
.所以![]() . (3分)
. (3分)
2.给定数据表
|
|
0 |
2 |
3 |
5 |
|
|
1 |
-3 |
-4 |
2 |
用牛顿插值求![]() 的不超过3次的插值多项式.
的不超过3次的插值多项式.
解:计算均差(6分)
|
x |
f(x) |
一阶均差 |
二阶均差 |
三阶均差 |
|
0 |
1 |
|
|
|
|
2 |
-3 |
-2 |
|
|
|
3 |
-4 |
-1 |
1/3 |
|
|
5 |
2 |
3 |
4/3 |
1/5 |
所以牛顿插值多项式为
![]() .
(1分)
.
(1分)
3.若线性方程组  的系数矩阵带误差,成为方程组
的系数矩阵带误差,成为方程组

(1)求原方程系数矩阵的条件数![]()
解:(1)![]() (3分)(2)对系数矩阵的扰动,估计解的相对误差
(3分)(2)对系数矩阵的扰动,估计解的相对误差 。
。
解:(2)![]()
 (4分)
(4分)
四.(15分)对方程组
(1)写出其Jacobi迭代格式,并说明该迭代格式是否收敛。(7分)
(2)写出题中方程组的Seidle迭代格式,取![]() ,迭代求出
,迭代求出![]() 。(8分)
。(8分)
解:(1)其Jacobi迭代格式为:
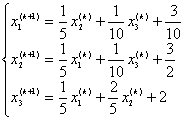 (5分)
(5分)
因为其系数矩阵严格对角占优,所以收敛(2分)
(2)解:其Seidel迭代格式为:
 (5分)
(5分)
![]() T ,
T ,
![]() T
(3分)
T
(3分)
五.(17分)对定积分![]() ,用龙贝格数值积分法计算I的近似值
,用龙贝格数值积分法计算I的近似值![]() .
.
|
|
0 |
1/8 |
1/4 |
3/8 |
1/2 |
|
|
1 |
0.9973978 |
0.9896158 |
0.9767267 |
0.9588510 |
|
|
5/8 |
3/4 |
7/8 |
1 |
|
|
|
0.9361556 |
0.9088516 |
0.8771925 |
0.8414709 |
|
(1) 已求得![]() .用变步长梯形公式的递推式计算
.用变步长梯形公式的递推式计算![]() . (8分)
. (8分)
解:(1)![]() .
(4分)
.
(4分)
![]() (4分)
(4分)
(2) 求![]() (4分)
(4分)
解:![]()
![]() (4分)
(4分)
(3) 求![]() (5分)
(5分)
解:![]() ;
(3分)
;
(3分)
![]() . (2分)
. (2分)
六.(15分)用改进的Euler公式,求初值问题![]() 在x1=0.1,x2=0.2,x3=0.3三结点处的数值解(即当x0=0,y0=1,h=0.1时,求出y1,y2,y3)
在x1=0.1,x2=0.2,x3=0.3三结点处的数值解(即当x0=0,y0=1,h=0.1时,求出y1,y2,y3)
解:改进的欧拉公式: (2分)
(2分)
初值x0=0,y0=1  (2分)
(2分)
x0=0,
y0=1,![]() (3分)
(3分)
x1=0.1,y1=1+0.05[1+1.2]=1+0.11=1.11 ![]() (3分)
(3分)
x2=0.2,y2=1.24205 ![]()
x3=0.3,y3=1.39846525 (2分)
2007~2008学年补考 参考答案
一.(8分)解: (1分)
(1分) (2分)
(2分)
 (2分)
(2分) (2分)
(2分)
回代解得 ![]() ,
,![]() ,
,![]() (1分)
(1分)
二.(10分)解:牛顿迭代格式为:![]() (1分);
(1分);
三种变形形式分别为:简单牛顿法 ![]() (1分)
(1分)
牛顿下山法 ![]() (1分)
(1分)
割线法![]() (1分)
(1分)
利用牛顿迭代法求解,将![]() 代入,得
代入,得
![]() (1分),
(1分),
![]() (1分)
(1分)
![]() (1分),
(1分),![]() (1分)
(1分)
所以取
![]() (2分)
(2分)
三.(22分)解:(1)先求Lagrange插值多项式
![]() (1分)
(1分)
![]()
![]() , (2分)
, (2分)
![]()
![]() (2分)
(2分)
![]()
![]() (2分)
(2分)
![]()
![]() (2分)
(2分)
![]()
![]() (1分)
(1分)
所以
![]() (1分)
(1分)
(2)再求Newton插值多项式
列均差表如下:

所以![]()
![]() (2分)
(2分)
![]() (1分)
(1分)
四.(10分)解:中心差分公式为 ![]() (2分)
(2分)
1)取h=0.01时, ![]() (4分)
(4分)
2)取h=0.02时, ![]() (4分)
(4分)
五.(20分)解:(1)其Jacobi迭代格式为 (5分)
(5分)
迭代矩阵为
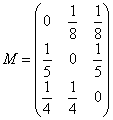 (2分)
(2分)
![]() <1 (2分) 所以Jacobi迭代格式收敛
(1分)
<1 (2分) 所以Jacobi迭代格式收敛
(1分)
(2)其Seidel迭代格式为:  (5分)
(5分)
将![]() 代入得
代入得 ![]() (3分)
(3分)
所以
![]() (2分)
(2分)
六.(15分)解:![]() (2分)
(2分)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() (9分)
(9分)

![]() (4分)
(4分)
七.(15分)解:改进的欧拉公式: (3分)
(3分)
将![]() 代入得
代入得  (2分)
(2分)
当x0=0,y0=0时, yp=0.2 (2分)
x1=0.2,y1=0.26,(2分) yp=0.604 (1分)
x2=0.4,y2=0.5928,(2分) yp=1.10991 (1分)
x3=0.6,y3=1.23344 (2分)