一.应力和应变

应力

定义：单位面积所受的力

工程应力的定义：

         A₀加载前的面积

 真实应力：

       A_i瞬时截面积

工程应变：

L0：厚长                      L1:加上载荷后的长度

ε真实应变=

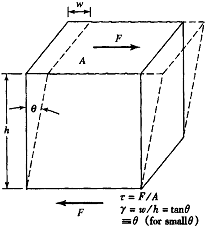
剪应力和剪应变

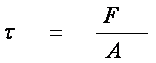
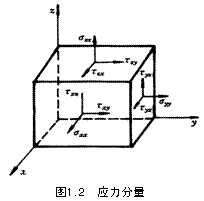
应力的规定如图

第一个字母表示应力

作用面的法线方向

第二个字母表示

作用力的方向

1.单向应力T

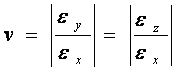
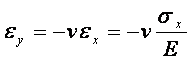
2.三向应力T

X方向变形

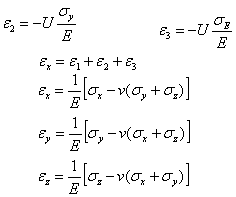
E   G       关系 

G=                   

3.体积弹性模量k
 长方体各棱长 a  b  c
 受力前体积

变形后

变形后体积   

K=

4.广义胡克定律：（各向异性体）

Ex≠Ey≠Ez

在单向受应力时，y、z两个方向的应变为：

弹性柔顺系数

同理

柔顺系数S的下标，十位数为应变方向，个位数为所受应力的方向。

    对于同时受有三向应力的各向异性材料，除正应力对应变有上述关系外，剪应力也会对正应变有影响。而且正应力  也会对剪应变  有影响，写成三向通式为

弹性柔度和弹性刚度系数各有36个   S_ij=S_ji，

这样，独立的系数只有21个  三斜晶系有21个弹性常数 单斜晶系  13个  斜方晶系 9个  四方晶系 7个   三方晶系 6个  六方晶系 5个   立方晶系 3个

三.弹性模量的物理本质及其影响因素

1. 弹性变形行为的微观描述

①  原子平面偏离平衡位置

②  键力发生变化，内力贮存

③  内力作用下，回到平衡位置

2. 弹性模量的本质

当r=r₀  F=0 平衡位置

=

结论：弹性模量的大小是原子间作用力——位移曲线在平衡位置时的斜率大小

本质：弹性模量是原子间键和强度的表征

3.影响弹性模量的因素

①原子结构的影响

②短周期，随原子序数的增加而降低

③同一族元素，随原子序数增加而降低

④过度族金属，都有高的弹性模量，外层价电子=

化合物 

⑤晶体结构

a.各向异性——面网距离

b.结构不同  E大小也不同

⑥温度

E0:OK时弹性模量   b=2.7～5.6

b T0: 试验常数   T0=180～230k

⑦两相系统的弹性模量

弹性应变能:单位体积所贮存的弹性能

上界模量Eu  假定:两相的应变相等    

  A:  V1   E1           B:  V2  E2

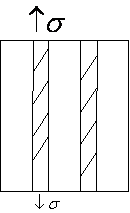
 下界模量  EL  假定：   E_L < E_实 < E_U

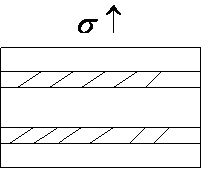
⑧气孔的影响

假定条件：a.气孔是球形   b.均匀分布  c.气孔的弹性模量

ⅰ.   适用于p较小的情况

ⅱ.

条件: 基体连续  气孔密闭

ⅲ .

条件: 基体连续  气孔密闭 V=0.3

ⅳ.

k₂ 试验常数   E₃ 基体模量

条件: 基体连续 各向同性 气孔大小 形状分布均无序

四.滞弹性

1.概述  力学模型

gh gf

2.关系式

   未驰豫模量

  驰豫模量

E_u > E_R

滞后部分变形  

: 材料的驰豫时间

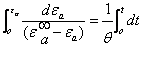
t：加载时间

当t<<时              得

当t>>时       得 E_R

用静态法则E时间长得E_R.用振动法时间短得

的物理意义:是表征固体材料滞弹性的物理量,从算起

到所经历的时间.

e =2.71828    

横波表示切变变形   可以测E  

纵波表压缩变形  

因为陶瓷材料变形很小,故很难测得,一般用物理学中波动法,振动法测得.

3.滞弹性产生的原因及研究目的

   原因:在弹性变形的过程中材料内部有物质迁移,点缺陷取向改变.杂质原子的扩散,晶界物质发生迁移.

研究目的:

   ①弹性常数的测定 

   ②材料的使用.滞弹性大,内部贮存能量大,材料内部要消耗能量.

③物质结构研究方法

在滞弹性情况下,存在交变应力时,在某一频率下,材料能耗最大,为能耗峰值,表示该材料中哪一种结构破坏,有物质发生迁移,不同材料其峰值不同,形成一个能耗图谱.实际材料都存在滞弹性,不是理想弹性体.

                                                         物质结构

宏观规律→本质→影响规律               显微结构

                                                         环境