主要内容
电导的物理现象
金属的导电性
半导体的电学性能
材料的介电性
材料的超导性
1. 电导的物理现象1.1 电导的宏观参数
• Flow of electrons in the metal to the positive electrode, as the effect of applying a voltage
• Simple picture of metallic bonding: high number of electrons in between the ions
• Energy scheme: Positive end of the rod has a lower energy than the negative end
•
Why not all the electrons move
to the positive terminal?
一、电阻率（电导率）
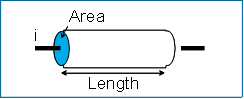
对一截均匀导电体，存在如下关系：
欧姆定律
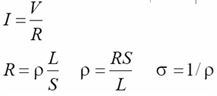
欧姆定律微分形式
二、表面电阻、体积电阻
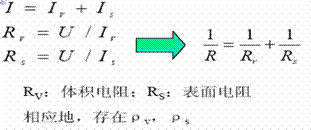
1. 对板状样品
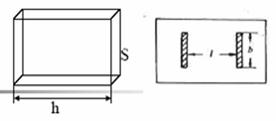
2. 对管状样品
3. 对圆片状样品
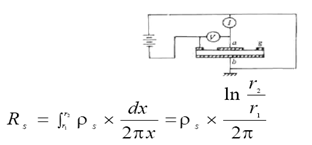
三、电阻测试方法
1. 二探针法（2-Probe Conductivity Measurements）
R = Rsample + Rcontact R = V/I r = (RA)/L
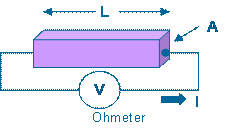特征：
适用于高导电率材料
消除电极非欧姆接触对测量的影响
Can give erroneous values if contact resistance, Rcontact, is not negligible with respect to Rsample
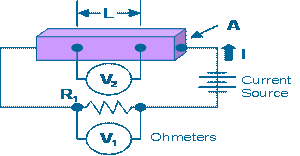2. 四探针法（4-Probe Conductivity Measurements）
I = V1/R1
Rsample
= V2/I
Rsample =
(V2R1)/V1
r = Rsample
(A/L)
特征：
样品尺寸较大一般用来测量半导体材料的方阻。
四、材料的电阻
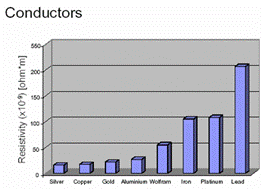
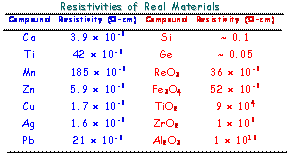
1.2 电导的物理特性
一、载流子
电流是电荷在空间的定向运动。
任何一种物质，只要存在带电荷的自由粒子——载流子，就可以在电场下产生导电电流。
金属中： 自由电子
无机材料中：
电子（负电子/空穴）——电子电导
离子（正、负离子/空穴）——离子电导
二、迁移率
三、霍尔效应
电子电导的特征是具有霍尔效应。
置于磁场中的静止载流导体，当它的电流方向与磁场方向不一致时，载流导体上平行于电流和磁场方向上的两个面之间产生电动势差，这种现象称霍尔效应。
霍尔系数（又称霍尔常数）RH
在磁场不太强时，霍尔电势差UH与激励电流I和磁感应强度B的乘积成正比，与霍尔片的厚度δ成反比，即
式中的RH称为霍尔系数，它表示霍尔效应的强弱。
霍尔效应的起源：
源于磁场中运动电荷所产生的洛仑兹力，
导致载流子在磁场中产生洛仑兹偏转。
该力所作用的方向即与电荷运动的方向
垂直，也与磁场方向垂直。
霍尔系数RH=μ*ρ，即霍尔常数等于霍尔片材料的电阻率ρ与电子迁移率μ的乘积。
霍尔系数RH有如下表达式：
对于半导体材料：
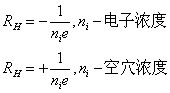
n型：
p型：
四、电解效应
离子电导的特征是具有电解效应。
利用电解效应可以检验
材料是否存在离子导电
可以半顶载流子是正离子还是负离子
2. 金属的导电性
2.1 金属导电机制
一、电阻率研究的重要性及前人的工作
纯金属电阻率理论研究是认识和理解电子与声子相互作用的最典型的例子之一,也是超导的理论基础。
包括J.Bardeen在内的不少人对纯金属电阻率与温度奇异的依赖关系进行过深入的理论研究，但“处理方法、数学积分及至结果表达式都是相当令人生畏的。” “The manipulation, integration and resulting expressions are rather formidable.” [R.J.Elliot and A.F.Gibson, AnIntroduction to Solid State Physics and its Applications, 311 (1976) ]，这些研究内容难以以基础课的内容向学生们讲授，高低温电阻率温度依赖性的奇异特性，其物理机理也不甚明了。
问题：能否用更简单明了的模型来揭示纯金属电阻率与温度的依赖关系？
基础一
第三章中晶格热容是一个宏观物理量，是晶格振动的统计平均效应。爱因斯坦采取了一个平均频率的简单模型，取得了很成功的结果。
电阻率也是一个宏观物理量，是电子与声子作用的统计平均效应。是否可采取平均声子的模型来处理纯金属电阻率问题呢？
所谓平均声子模型，是假定声子系统由平均声子来构成，在这个系统中，每个声子的动量等于原声子系统中声子的平均动量。
我们知道，对电导有贡献的只是费密面上的电子，因此纯金属电阻率可看成是费密面上的电子与平均声子相互碰撞的结果。
基础二
已知，立方晶系金属的电阻率
（1）
电子浓度
，电子电荷 e ， 而费密面上电子的有效质量
可看成与温度无关。可见电阻率与温度的依赖关系，取决于弛豫时间
的倒数与温度的依赖关系。由固体物理知识可知. 
二、金属自由电子论
采用平均声子模型, 上式简化成
（2）
其中是一常数，是除
态外，费密面上
其它电子态的总和，
是电子与一个平均声子碰撞所产生的散射角。因此，对 的分析，就转换成对因子
和
的分析。费密面附近电子的平均速度
,是一常数;按照德拜模型,声子的速度为金属的声速,也是常数。所以
2.求
考虑正常散射过程，由下图可知
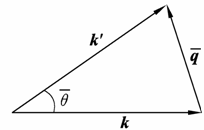
于是（2）式变成
电阻率变成
(3)
因为
是声子的平均动量，由此推出重要结论：
纯金属的电阻率与声子浓度和声子平均动量的平方
成正比。
声子的平均动量
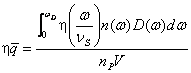(5)
取变量变换
将以上诸式代入(3)式得
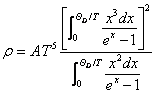(6)
其中常数
高温时, x=（
/T ）®0 ，ex »1+x,得到
(7)
在甚低温时, x=（ /T ）® 
,得到
r=
(
8)
可见由平均声子模型得到的理论结果与实验规律是相符的.
小 节
本节是认识和理解电子与声子相互作用的最典型的例子之一。
费密面上的电子遭受声子散射是纯金属具有电阻率的根源。
纯金属的电阻率与声子浓度和声子平均动量的平方成正比。此结论把纯金属的电阻率与声子的参数联系了起来。
三、马基申定则（Matthissen’s Law）
2.2 温度对电阻率的影响
2.3 压力对电阻率的影响
2.4 固溶体的导电性
3. 半导体的导电性
3.1 半导体的能带结构
3.2 本征半导体与杂质半导体
一、本征半导体
二、杂质半导体
3.3 p-n结的整流特性
一、p-n结的定义
二、p-n结的结构
三、p-n结的物理本质
3.4 晶体管的放大效应
一、晶体管的类型
二、晶体管的结构
三、晶体管的工作原理
4. 材料的介电性
4.1 电介质概述
一、电介质的定义
电介质的本质特征是以极化的方式传递、存储或记录电场的作用和影响，介电常数是表征电介质的最基本的参量。
陶瓷的介电性能决定于感应极化的产生及其随时间的建立过程，而介电常数随频率和温度的变化是决定电介质应用的重要因素。
在讨论电介质的极化时，通常针对各向同性线性均匀电介质在电场中的行为。
所说的均匀是指电介质的性质不随空间坐标发生变化，
所说的各向同性是指电介质的参数不随场量的方向发生变化，
线性是指电介质的参数不随场量的数值发生变化。
二、电介质材料
高频电容器陶瓷（即I类介质陶瓷）和微波介质陶瓷，通常都是线性电介质。
而铁电体（铁电陶瓷）则表现出电学非线性，通常称为非线性电介质。
单晶材料为各向异性电介质，陶瓷材料通常被视为各向同性电介质，但经极化处理后的压电陶瓷则表现出各向异性。
各向异性电介质通常用张量来描述其物理性质。
一、电介质的极化定义
导体中的自由电荷在电场作用下定向运动，形成传导电流。但在电介质中，原子、分子或离子中的正负电荷则以共价键或离子键的形式被相互强烈地束缚着，通常称为束缚电荷。
在电场作用下，正、负束缚电荷只能在微观尺度上作相对位移，不能作定向运动。正负束缚电荷间的相对偏移，产生感应偶极矩。在外电场作用下, 电介质内部感生偶极矩的现象，称为电介质的极化。
注意：铁电体中自发极化的产生是不需要外加电场诱导的，完全是由特殊晶体结构诱发的。
电介质在电场作用下的极化程度用极化强度矢量P表示，极化强度P是电介质单位体积内的感生偶极矩，可表示为：
极化强度的单位为库仑/米2
(C/m2)
每个分子的电偶极矩
注意: 介质极化也有均匀极化与非均匀极化之分。
1.真空中 P = 0 ，真空中无电介质。
2.导体内 P = 0 ，导体内不存在电偶极子。
3. 电偶极子排列的有序程度反映了介质被极化的程度，排列愈有序说明极化愈烈
二、极化类型
电子位移极化（Electronic Polarizability）
Response is fast, Response is fast, τ is small
弹性位移极化
（瞬时极化）
离子位移极化（Ionic Polarizability）
Response is slower
偶极子取向极化（Dipolar
Polarizability）
Response is still slower
取向极化
（弛豫极化）
空间电荷极化(Space Charge Polarizability)
Response is quite slow, τ is large
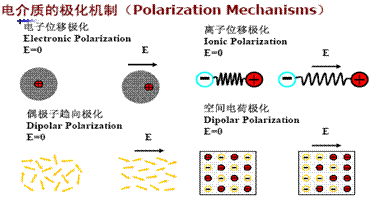
注意：
原子和离子的电子位移极化率与温度无关。
离子位移极化率与正负离子半径和的立方成正比，与电子位移极化率有大体相同的数量级，随温度升高，离子间距离增大，相互作用减弱，力常数K减小，因此离子位移极化率随温度升高而增大，但增加甚微。
偶极子取向极化率与温度成反比，随温度升高而下降。偶极子取向极化率比电子位移极化率大得多，约为10－
介电性能的温度特性对于介电材料的实际应用至关重要，如介电常数温度系数是衡量电介质陶瓷性能的重要指标之一。
不同电介质因极化机制不同, 通常表现出不同介电常数.
气体: 单原子, 电子位移极化, er =
1+ n0a/e0
极性分子气体: a=ae+am=ae+m02/3KT
非极性液体和固体电介质, er=2~2.5
极性液体电介质, a=ae+am=ae+m02/3KT,er>2.5
离子晶体
4.3 电介质的物理参数
一、基本介电关系
在各向同性的线性电介质中, 极化强度P与电场强度E成正比，且方向相同，即
P = cε0E
c---电介质的极化率， 对于均匀电介质c是常数，对于非均匀电介质则是空间坐标的函数。c定量表示电介质被电场极化的能力，是电介质宏观极化参数之一。
基本介电关系：电位移矢量与电场强度和极化强度之间的关系为: D = e0E+P,适用于各类电介质。
D = e0E+P＝e0E＋ec0E＝（1＋c）e0E, 令（1＋c）e0＝e0er=e，
则有D = eE, 仅适用于各向同性线性电介质
e 和er分别为电介质的介电常数和相对介电常数。
电介质极化的宏观参数与微观参数的关系
从微观上, 极化强度是电介质单位体积中所有极化粒子偶极矩的向量和, P = n0.m,
对线性极化, m=aEe, a---原子分子离子的极化率, Ee---有效电场
上式表示了电介质中与极化有关的宏观参数(c、er、E）与微观参数(a、n0、Ee)之间地关系。
二、介电常数
在交变电场下，由于介质的极化建立需要一定时间，在实际电介质中会产生损耗，因此介电响应需用复介电常数描述
其中，
表示损耗，称为损耗因子，是表示电介质损耗的特征参数，其中g 为电导率。在实际应用中，通常用损耗角正切表示电介质在交变电场下的损耗，
三、介电弛豫
弛豫过程：一个宏观系统由于周围环境的变化或受到外界的作用而变为非热平衡状态，这个系统再从非平衡状态过渡到新的热平衡态的整个过程就称为弛豫过程。
弛豫过程实质上是系统中微观粒子由于相互作用而交换能量，最后达到稳定分布的过程。弛豫过程的宏观规律决定于系统中微观粒子相互作用的性质。因此，研究弛豫现象是获得这些相互作用的信息的最有效途径之一。
四、介电损耗
电介质在电场作用下的往往会发生电能转变为其它形式的能（如热能）的情况，即发生电能的损耗。常将电介质在电场作用下，单位时间消耗的电能叫介质损耗。
4.4 电介质的击穿
电介质的击穿 一般外电场不太强时，电介质只被极化，不影响其绝缘性能。当其处在很强的外电场中时，电介质分子的正负电荷中心被拉开，甚至脱离约束而成为自由电荷，电介质变为导电材料。当施加在电介质上的电压增大到一定值时，使电介质失去绝缘性的现象称为击穿(breakdown)。
击穿场强——电介质所能承受的不被击穿的最大场强。
击穿电压——电介质（或电容器）击穿时两极板的电压。
5. 材料的超导性
5.1 超导特性
什么是超导体？
1. 零电阻
将超导体冷却到某一临界温度（TC）以下时电阻突然降为零的现象称为超导体的零电阻现象。不同超导体的临界温度各不相同。例如，汞的临界温度为4.15K（K为绝对温度，0K相当于
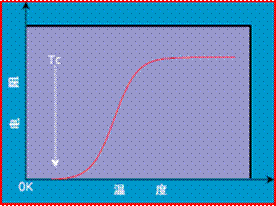
2. 完全抗磁性
当超导体冷却到临界温度以下而转变为超导态后，只要周围的外加磁场没有强到破坏超导性的程度，超导体就会把穿透到体内的磁力线完全排斥出体外，在超导体内永远保持磁感应强度为零。超导体的这种特殊性质被称为“迈斯纳效应”。
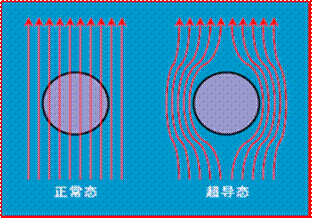迈斯纳效应与零电阻现象是超导体的两个基本特性，它们既互相独立，又密切联系。
3. 超导态的临界参数
温度（TC）——超导体必须冷却至某一临界温度以下才能保持其超导性。
临界电流密度（JC）——通过超导体的电流密度必须小于某一临界电流密度才能保持超导体的超导性。
临界磁场（HC）——施加给超导体的磁场必须小于某一临界磁场才能保持超导体的超导性。
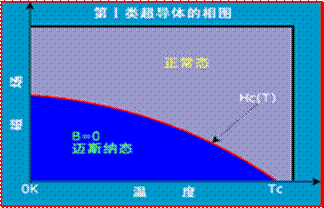
以上三个参数彼此关联，其相互关系如下图所示。
5.2 超导体分类
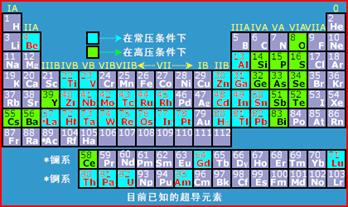
目前已查明在常压下具有超导电性的元素金属有32种（如下图元素周期表中青色方框所示），而在高压下或制成薄膜状时具有超导电性的元素金属有14种（如下图元素周期表中绿色方框所示）。
第I类超导体
第I类超导体主要包括一些在常温下具有良好导电性的纯金属，如铝、锌、镓、鎘、锡、铟等，该类超导体的溶点较低、质地较软，亦被称作“软超导体”。其特征是由正常态过渡到超导态时没有中间态，并且具有完全抗磁性。第I类超导体由于其临界电流密度和临界磁场较低，因而没有很好的实用价值。
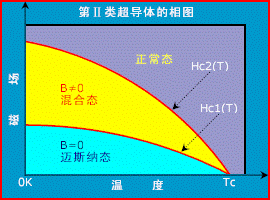
第II类超导体
除金属元素钒、锝和铌外，第II类超导体主要包括金属化合物及其合金。第II类超导体和第I类超导体的区别主要在于：
1) 第II类超导体由正常态转变为超导态时有一个中间态（混合态）
2) 第II类超导体的混合态中有磁通线存在，而第I类超导体没有；
3) 第II类超导体比第I类超导体有更
第II类超导体根据其是否具有磁通钉扎中心而分为理想第II类超导体和非理想第II类超导体。
理想第II类超导体的晶体结构比较完整，不存在磁通钉扎中心，并且当磁通线均匀排列时，在磁通线周围的涡旋电流将彼此抵消，其体内无电流通过，从而不具有高临界电流密度。
非理想第II类超导体的晶体结构存在缺陷，并且存在磁通钉扎中心，其体内的磁通线排列不均匀，体内各处的涡旋电流不能完全抵消，出现体内电流，从而具有高临界电流密度。在实际上，真正适合于实际应用的超导材料是非理想第II类超导体。
