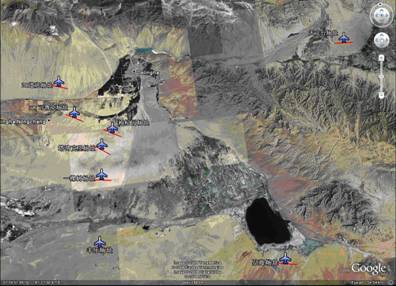
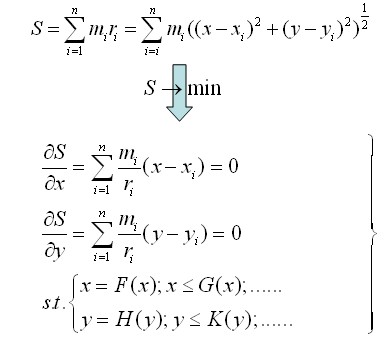第六章 厂址最优位置确定的方法 |
| 第一节 厂址优选方法概述 |
| 第二节 比较矩阵法 |
| 第三节 模糊综合评判法 |
| 第四节 判定优先次序法 |
| 研究进展 |
|
第一节 厂址优选方法概述 |
一、厂址优选方法分类 各类厂址优选方法基本上可以分为两大类： 第 I 类：没有候选的厂址位置，通过建立基于某种或某几种目标的数学模型，在空间中直接寻求最优厂址位置，如重心法及数学程序法、数学规划法; 第 II 类：首先通过定性分析建立候选厂址位置集合，进而通过分析候选集合中各厂址的各项指标(包括定性指标与定量指标)，得到各厂址的综合评价值，并在其中择优作为确定的厂址最优位置。如比较矩阵法、层次分析法、判定优先次序法等。 二、两类方法比较 第 I 类方法是完全定量分析过程，客观性很高，在理论上具有很强的说服力;第 II 类方法是定性定量相结合的分析过程，实用性突出，在实践中得到了比较广泛的应用。 选厂过程中考虑因素的多寡，决定着构造厂址优选数学模型以及求解这些模型的难易程度。 规划选厂阶段考虑因素较少;工程选厂阶段考虑因素甚多。 综上，第 I 类方法适用于规划选厂阶段;第 II 类方法适用于工程选厂阶段。
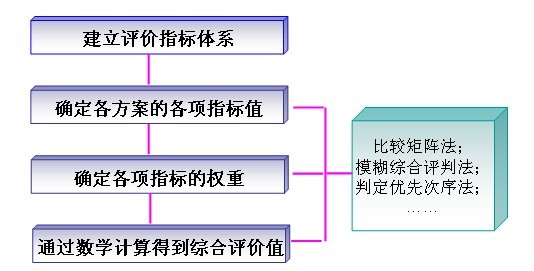
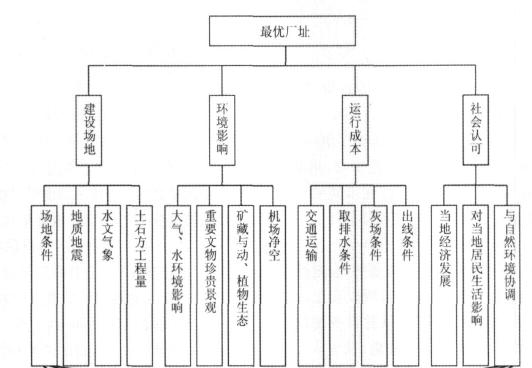
三、第II类方法的基本思路
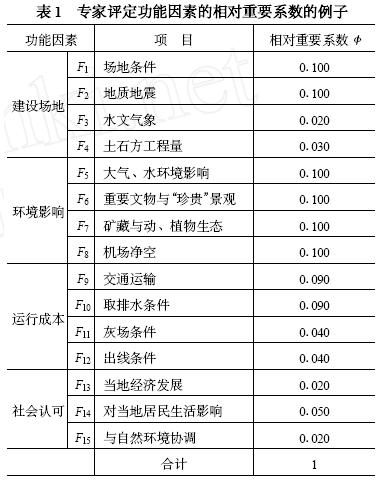
—— 火力发电企业厂址选择评价指标（柯恩龙 2007） |
第二节 比较矩阵法 |
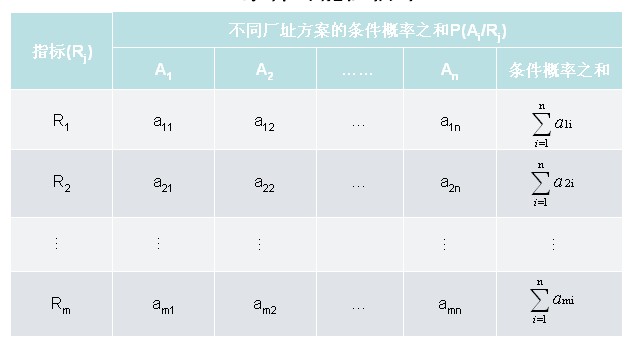
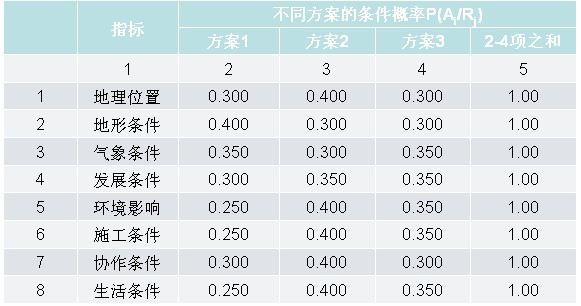
一、基本思路 将评价指标分为定量与定性两大类; 定量指标的数值全部以费用计，单位为“元”，无需给定各指标的权重系数，就可得到每个方案对于定量指标的总价值分S1; 定性指标的数值均以条件概率P(Ai/Rj)表示，各指标的权重系数人为给定，计为概率P(Rj); 每个方案对于定性指标的总价值分S2为：各定性指标以上两个概率的结合概率P(Ai/Rj)* P(Rj)之和; 将S1、S2作为指标值，并人为给定定量与定性指标的权重，再次计算结合概率就得到每个方案的最终价值分。 条件可能性估计
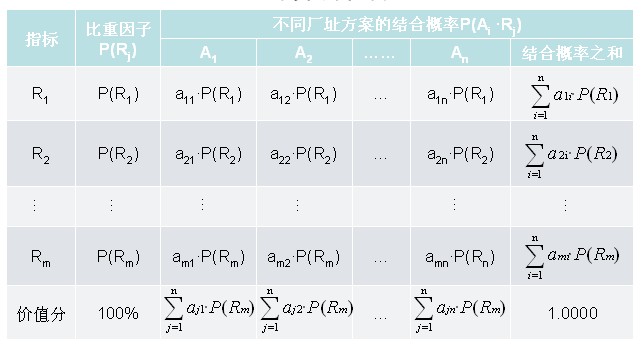
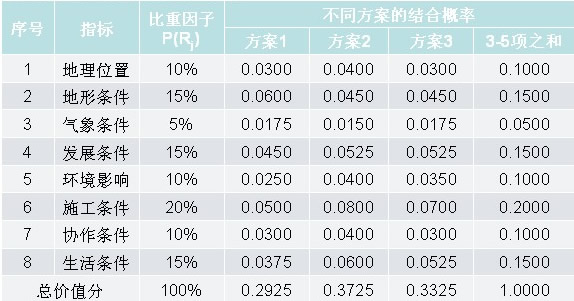
计算价值分
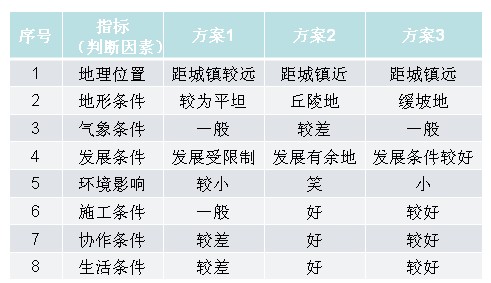
二、算例 厂址方案比较表示例 条件可能性估计示例 计算价值分析示例
|
第三节 模糊综合评判法 |
一、基本思路 模糊综合评判方法，是近年来逐渐推广应用的一种系统综合评价方法。是综合运用层次分析法(AHP)与模糊数学方法(Fuzzy)而形成的一种系统综合评价方法。模糊综合评判的实施步骤如下： (1) 确定评价系统的评审要素集合：
(2) 确定各评审要素的权系数行向量： (3) 确定评价基准及相应的价值量：
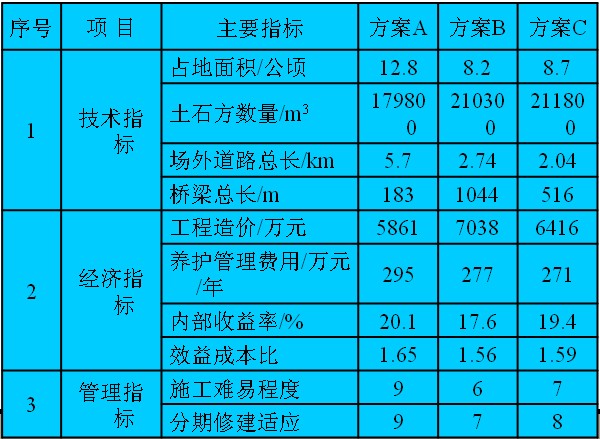
(4) 计算评价系统关于各评审要素的模糊综合评判矩阵： (5) 对模糊综合评判矩阵进行加权，得出模糊综合评价结果： (6) 计算各评价系统的可行度： (7) 比较各系统的可行度，按可行度的大小排出先后次序。 特别需要注意的是，模糊综合评判可以在不同的层次上反复进行，低一层次的结果可以作为高一层次的基础数据，从而实现多级模糊综合评判。 二、算例
首先在基础层级内对于各单项指标分别做模糊综合评判。以技术指标一项为例，计算过程如下： 计算隶属度
进而确定模糊综合评判矩阵：
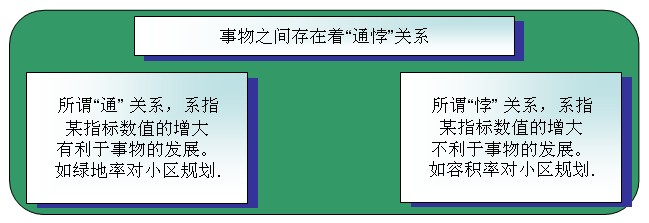
对于具有通关系的指标，其R的要素即 对于具有悖关系的指标，其R的要素为 因此有判断矩阵：
取权值向量为
故对于技术指标一项而言，评价值顺序为：C、B、A 类似地，对经济指标有：
评价值顺序为：A、C、B。 对管理指标有：
评价值顺序为：B与C、A。 接下来，以
即综合评价值顺序为：方案C、方案B、方案A。故，选择方案C作为厂址推荐方案。
|
( 
为表1中各特性指标的数值)
，可以计算方案的单项指标评价值：
、
、
为基础数据，并选取权向量，做高一层极的模糊综合评判，确定综合最优方案。
第四节 判定优先次序法 |
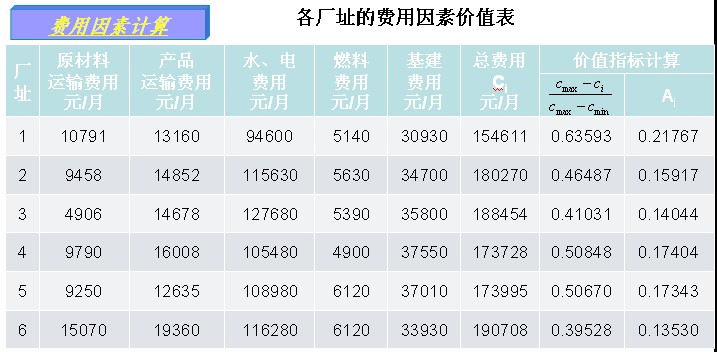
一、基本步骤 1. 确定关键因素价值指标 对于厂址i，只要其关键要素中有一个不能满足，则该厂址方案应予摒弃。 2. 费用因素与定性因素的价值指标
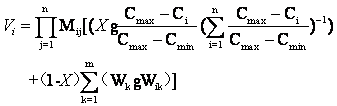
1)费用因素的价值指标 其中： 2)定性因素的价值指标
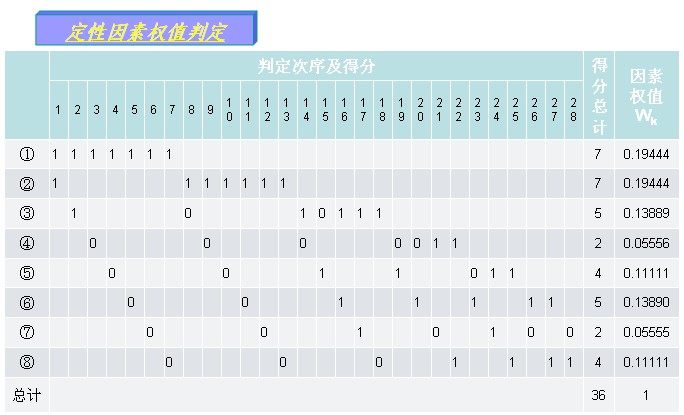
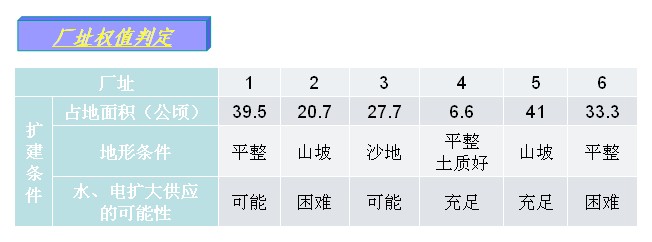
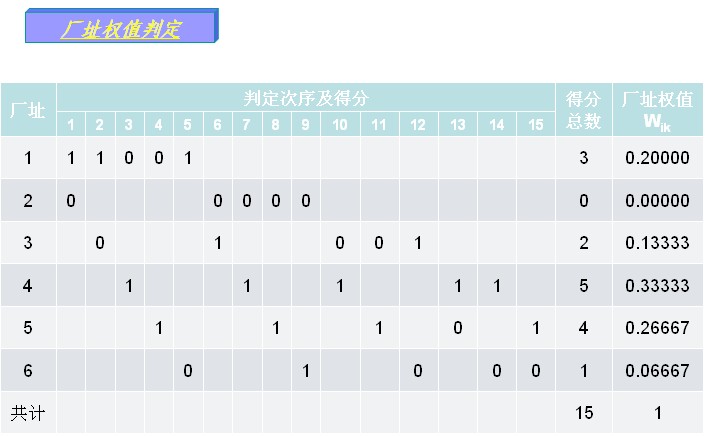
其中， 确定权值采用“判定优先次序法”。 两两比较各个因素(或厂址)，可能得到如下结果： a.第一个因素比第二个因素重要，则第一个因素得1分，第二个因素得0分; b.第二个因素比第一个因素重要，则第二个因素得1分，第一个因素得0分; c.两者同样重要，各得1分(只可能是因素比较)。 统计各个因素(或厂址)的总得分
于是有：
而 另外，如因素(或厂址)为n个，则总判定次数为：
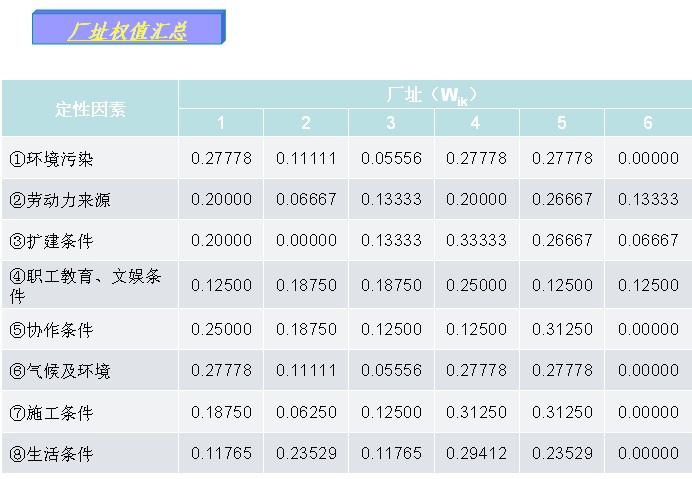
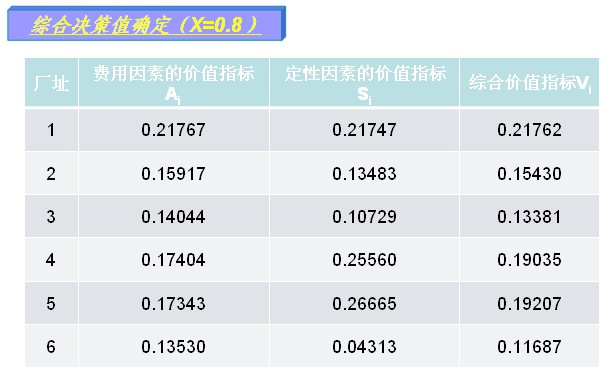
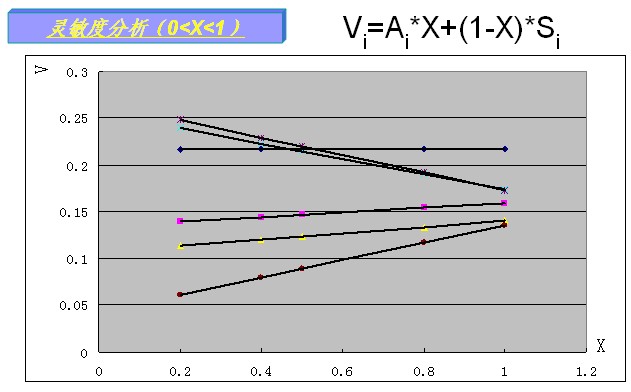
判定优先次序的计算过程一般列表进行，见算例。 3. 综合决策值的确定 由决策人员人为选定费用因素决策权 综合决策值为：
二、算例 |
;
为厂址i的第j个关键因素的价值指标，有：
;
：
为厂址i各项费用因素的总费用; 
为允许的最大值; 
为可能出现的最小费用; 
且 
，这就为费用因素和定性因素两者的价值指标提供了可比条件。
为第K个定性因素的因素权值; 
为厂址权值。
，于是定性因素决策权为
;
 |
研究进展 |