课后习题

第三章第三题答案

答：离散沃尔什变换
当N=2n 时，可以得到函数 f(x) 的离散沃尔什（ Walsh ）变换（ W （ u ））：

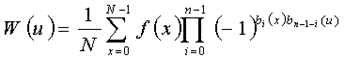
bk(z)是z的二进制表达式列中的第k位。例如n=3,则对z=6,其二进制数为110，有b0(z)=0，b1(z)=1，b2(z)=1。
由沃尔什变换核组成的矩阵是一个对称矩阵，且其行和列正交。这些性质表明反变换与正变换核只差1个常数1/N，即：

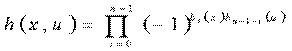
所以离散沃尔什反变换为：

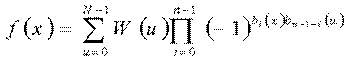
由于一维沃尔什变换正变换和反变换只差一个常数项1/N，所以用于正变换的算法也可用于反变换。一维沃尔什正变换和反变换核由以下两式给出：

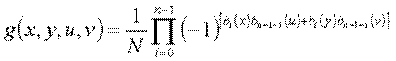
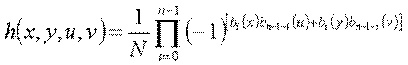
离散哈达玛变换
哈达玛变换与沃尔什变换相似，所以有些参考书上把二者统称为沃尔什-哈达玛变换。
（一）一维离散哈达玛变换
当N=2n 时，一维哈达玛正变换核和反变换核相似。一维哈达玛变换对可表示为：

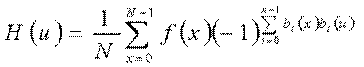
             (u = 0,1,2,…, N-1)

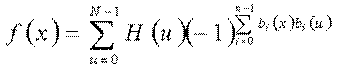
               (x = 0,1,2,…, N-1)
哈达玛变换核除了因子1/N之外，由一系列的+1和-1组成。如N=8时的哈达玛变换核用矩阵表示为：

由此矩阵可得出一个非常有用的结论，即2N阶的哈达玛变换矩阵可由N阶的变换矩阵按下述规律形成：

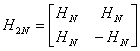
而最低阶（N=2）的哈达玛变换矩阵为：